[프로그래머스] 단어 변환 - DFS(깊이 탐색) 방식(feat.cpp)

문제 내용
문제 설명
두 개의 단어 begin, target과 단어의 집합 words가 있습니다. 아래와 같은 규칙을 이용하여 begin에서 target으로 변환하는 가장 짧은 변환 과정을 찾으려고 합니다.
|
1. 한 번에 한 개의 알파벳만 바꿀 수 있습니다. |
예를 들어 begin이 hit, target가 cog, words가 [hot, dot, dog, lot, log, cog]라면 hit-> hot -> dot -> dog -> cog와 같이 4단계를 거쳐 변환할 수 있습니다.
두 개의 단어 begin, target과 단어의 집합 words가 매개변수로 주어질 때, 최소 몇 단계의 과정을 거쳐 begin을 target으로 변환할 수 있는지 return 하도록 solution 함수를 작성해주세요.
제한사항
-
각 단어는 알파벳 소문자로만 이루어져 있습니다.
-
각 단어의 길이는 3 이상 10 이하이며 모든 단어의 길이는 같습니다.
-
words에는 3개 이상 50개 이하의 단어가 있으며 중복되는 단어는 없습니다.
-
begin과 target은 같지 않습니다.
-
변환할 수 없는 경우에는 0을 return 합니다.
입출력 예
| begin | target | words | return |
| hit | cog | [hot, dot, dog, lot, log, cog] | 4 |
| hit | cog | [hot, dot, dog, lot, log] | 0 |
문제 설명
begin을 target으로 바꾸는 방법 중 최소의 비용으로 바꿀 수 있는 방법을 알아내라는 문제입니다.
조건부터 다시 풀어 적어보겠습니다.
첫 번째 조건인 "한 번에 한 개의 알파벳만 바꿀 수 있습니다." 이 말을 다른 말로 하자면 begin의 값과 바뀔 문자가 서로 한 글자만 다르다는 뜻입니다.
그리고 조금 더 생각해 보셔야 할 조건인 두 번째 조건인 "words에 있는 단어로만 변환할 수 있습니다."은 첫 번째 조건과 같이 생각해보자면 "내가 고를 수 있는 words는 한 글자만 다른 words입니다" 이런 식으로 생각할 수 있습니다.
하지만 내가 고를 수 있는 문자가 한 개로 한정되어 있지 않습니다.
위에 예제로 예를 들자면 값이 hit인 begin 변수가 바뀔 수 있는 words는 hot입니다.
그렇다면 hot에서 변할 수 있는 words는 dot와 lot 두 개 나 존재합니다.
이 처럼 값을 선택할 때마다 경우의 수는 한 개가 아니라 여러 개가 나올 수 있습니다.
그리고 그중에서 최소로 변환해야 할 경우를 알아내야 한다는 것입니다.
이렇게 값을 찾아내는 것을 보통 탐색이라고 합니다.
하지만 그냥 탐색만으로는 이전 값들의 경우의 수들도 다 확인하기는 힘듭니다.
하지만 이런 탐색은 가능하지 않을까요?
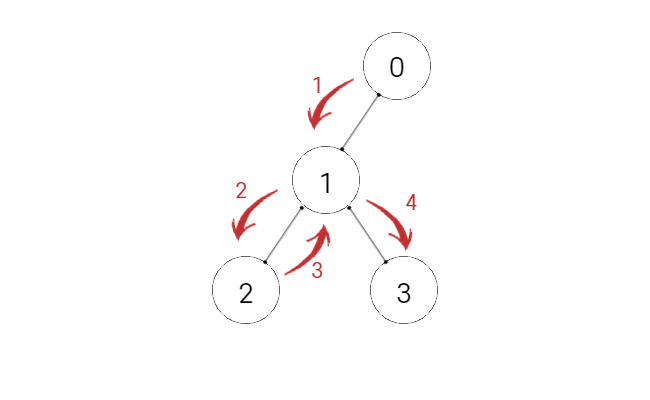
위 그림은 DFS, 깊이 탐색 방법입니다.
이 방법을 에서 O안에 저장된 값들만 쏙 바꿔 보겠습니다.

깊이 탐색 중 일부를 잘라서 보고 있긴 하지만 이것만 봐도 전체 경우의 수를 모두 탐색할 수 있을 거 같지 않나요?
그럼 어떻게 풀어야 할지 알았으니 하나하나 c++을 사용하여 코드를 만들어 보겠습니다.
구현
첫째로 깊이 탐색을 하는데 생각해야 할 점은 같은 곳을 중복해서 들리면 안 되도록 해줘야 합니다.
그래서 그것을 체크해주는 변수부터 만들어 주어야 됩니다.
answer : 리턴 값 (51로 초기화되어있는 이유는 이 문제의 경우의 수 중 나올 수 없는 값입니다.)
size : words 배열 크기 변수
w_size : 문자열의 길이 변수
int solution(string begin, string target, vector<string> words){
int answer = 51;
const int size = words.size();
const int w_size = words[0].size();
vector<bool> checked(size, false);
...
}저는 항상 이런 식의 탐색을 할 때는 탐색을 완료했다는 checked 나 visited 변수를 만들어 사용합니다.
그럼 깊이 탐색을 위한 변수도 만들었겠다 이제 생각해볼 것은 어떤 words로 시작을 할까입니다.(시작점 정하기)
어떤 것으로 시작하냐에 따라 또 값들이 다 달라질 수 있기 때문입니다.
그렇다면 words의 길이만큼 반복을 하면서 begin문자열과 한 글자만 다른 문자열을 선택하면 되겠습니다.
count : 문자가 서로 다를 경우 카운팅 해주는 변수
DFS : 재귀적으로 깊이 탐색할 함수
track : 재귀 함수를 돌면서 개수를 세어줍니다.
int solution(string begin, string target, vector<string> words){
...
for(int i = 0; i < size; ++i){
int count = 0;
for(int j = 0; j < w_size; ++j)
if(begin[j] != words[i][j])
++count;
if(count == 1){
// 문자 한 개만 다르다면...
checked[i] = true;
int track = 0;
answer = min(answer, DFS(words[i], target,
words, size, w_size,
checked, track) + 1);
checked[i] = false;
}
}
...
}(재귀적으로 돌고 나온 값에 +1을 해준 이유는 처음에 시작할 값을 정할 때 한번 변환했기 때문입니다.)
자, 그러면 이제 깊이 탐색을 위한 시작점을 정하였고, DFS 함수를 통하여 그 시작점에 대해 완전 탐색을 할 수 있게 되었습니다.
그렇다면 이제 깊이 탐색(DFS 함수 내부)을/를 구현하면 되겠군요.
int DFS(const string start, const string target,
const vector<string> words, const int size, const int w_size,
vector<bool> & checked, int track){
if(start == target){
return track;
}
int ret = 51;
for(int i = 0; i < size; ++i){
if(checked[i] == false){
int count = 0;
for(int j = 0; j < w_size; ++j)
if(start[j] != words[i][j])
++count;
if(count == 1){
checked[i] = true;
ret = min(ret, DFS(words[i], target, words, size, w_size, checked, ++track));
--track;
checked[i] = false;
}
}
}
return ret;
}
혹시 이 함수의 구조 중 아까 저희가 만들었던 코드가 비슷해 보이지 않습니까?
그 이유는, 처음 저희가 시작 값을 정할 때와 다음에 어떤 값을 정하는 조건이 같기 때문입니다.
그렇기 때문에 코드가 비슷한 것입니다.
이렇게 재귀 함수가 돌다가 딱 start 문자열과 target 문자열이 같아지는 순간 몇 번째에 문자열이 같아졌는지 반환합니다.
만약에 같아지는 순간이 없다면 (변환되지 않았다면) 반환 값이 51이겠지요?
문제 내용에서 보면 변환이 안될 경우 0을 반환해 달라고 요구 사항이 있었으니 값이 51일 때 0을 반환해주는 코드를 작성하면 되겠군요!
int solution(string begin, string target, vector<string> words){
...
if(answer == 51)
answer = 0;
return answer;
}
전체 코드
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int DFS(const string start, const string target,
const vector<string> words, const int size, const int w_size,
vector<bool> & checked, int track){
if(start == target){
return track;
}
int ret = 51;
for(int i = 0; i < size; ++i){
if(checked[i] == false){
int count = 0;
for(int j = 0; j < w_size; ++j)
if(start[j] != words[i][j])
++count;
if(count == 1){
checked[i] = true;
ret = min(ret, DFS(words[i], target, words, size, w_size, checked, ++track));
--track;
checked[i] = false;
}
}
}
return ret;
}
int solution(string begin, string target, vector<string> words){
int answer = 51;
const int size = words.size();
const int w_size = words[0].size();
vector<bool> checked(size, false);
for(int i = 0; i < size; ++i){
int count = 0;
for(int j = 0; j < w_size; ++j)
if(begin[j] != words[i][j])
++count;
if(count == 1){
// 문자 한 개만 다르다면...
checked[i] = true;
int track = 0;
answer = min(answer, DFS(words[i], target,
words, size, w_size,
checked, track) + 1);
checked[i] = false;
}
}
if(answer == 51)
answer = 0;
return answer;
}
테스트 코드 (필요하신 분만)
int main(){
const vector<string> begin_testcases = {
"hit", "hit"
};
const vector<string> target_testcases = {
"cog", "cog"
};
const vector<vector<string>> words_testcases ={
{"hot", "dot", "dog", "lot", "log", "cog"},
{"hot", "dot", "dog", "lot", "log"}
};
for(int i = 0; i < begin_testcases.size(); ++i){
const int ret = solution(begin_testcases[i], target_testcases[i], words_testcases[i]);
cout << ret << endl;
cout << "===================" << endl;
}
return 0;
}
끝맺음
프로그래머스 문제인 단어 변환을 풀어보면서 깊이 탐색이라는 것을 알아봤습니다.
하지만 이 방법은 하나하나 모든 경우의 수를 살펴보기 때문에 길이가 길어질수록 시간이 오래 걸립니다.
그래도 어느 한 문제를 풀기에는 강력한 알고리즘인 것은 틀림없기에 기억해 두시면 좋을 거 같습니다.
또 제가 푸는 방법이 최고의 방법은 아니기에 항상 많은 지적을 해주시면 감사하겠습니다.

'알고리즘' 카테고리의 다른 글
| [Boyer-Moore] 문자열 탐색 ! 보이어-무어 알고리즘(feat.cpp) (0) | 2020.11.07 |
|---|---|
| [KMP] 카누스 모리스 프렛 알고리즘 (feat.cpp) (0) | 2020.11.04 |
| 트라이 알고리즘이란 ? (feat.cpp) (0) | 2020.11.03 |
| [프로그래머스] 위장 (0) | 2020.11.02 |
| [heap] 힙 이란? (feat.cpp) (0) | 2020.11.01 |
[Boyer-Moore] 문자열 탐색 ! 보이어-무어 알고리즘(feat.cpp)
문자열 탐색
보이어 무어 알고리즘은 KMP 알고리즘과 같이 대표적인 문자열 탐색 알고리즘입니다.
문자열을 탐색할 시 고지식한 알고리즘(완전 탐색 알고리즘)을 사용할 시 상당한 길이가 짧은 문자열일 경우에는 상관없지만 그의 길이가 길어질수록 상당한 시간이 소요됩니다.
그러한 시간 복잡도 문제를 해결하기 위한 대표적인 알고리즘 두 개가 KMP 알고리즘과 이번에 알아볼 보이어-무어 알고리즘입니다.
KMP 알고리즘과 보이어-무어 알고리즘은 보이어-무어 알고리즘은 상당히 비슷한 메커니즘을 갖고 있습니다.
고지식한 알고리즘은 다음 인덱스로 한 칸씩 이동하는 반면 KMP 알고리즘과 보이어-무어 알고리즘은 미리 정의해둔 테이블을 참조하여 다음에 비교할 위치로 건너뛰어 버립니다.
이러한 행위는 반복 횟수를 상당히 줄일 수 있습니다.
그렇다면 보이어-무어 알고리즘은 어떤 방식으로 문자열을 건너뛰게 되는지 이제부터 알아가 보겠습니다.
보이어-무어 알고리즘
기존 고지식한 알고리즘과, KMP 알고리즘 혹은 지금까지 봐왔던 알고리즘들은 대부분 처음부터 비교해 나갈 것입니다.
하지만 보이어-무어 알고리즘은 뒤에서부터 비교해나갑니다.
뒤에서부터 비교를 진행해 나가다 비교 값이 서로 다를 시 테이블을 참조해 나아갑니다.
아래는 보이어-무어 알고리즘으로 비교해 나아가는 이미지입니다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| m | a | b | c | a | b | a | b | c | d |
| n | a | b | c | d |
뒤에서 비교하다 index 3번이 다르다는 것을 확인 후 테이블을 참조합니다.
테이블을 참조 후 다음 비교할 위치로 건너뜁니다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| m | a | b | c | a | b | a | b | c | d |
| n | a | b | c | d |
그다음 값을 보면 index 5, 6번이 다르지만 보이어-무어 알고리즘은 뒤에서부터 비교하므로 테이블 참조 시 index 6번에 대한 값을 참조하여 다음 비교 위치로 넘어갑니다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| m | a | b | c | a | b | a | b | c | d |
| n | a | b | c | d |
총 2번의 이동만으로 원하는 값을 찾아냈습니다.
만약 고지식한 알고리즘이었다면 2번 이동했을 때쯤 index 2번에 n의 문자열이 위치했습니다.
그럼 아까부터 언급하고 계속 참조했던 테이블에 대하여 알아보겠습니다.
생략 테이블
생략 테이블은 제가 설명하기 쉽게 붙인 이름입니다.
패턴 문자열을 찾기 위해 패턴 문자열에 대해 생략 테이블이 2개가 필요합니다.
첫 번째로는 Bad Character Heuristica 방식으로 테이블을 생성합니다.
영어 그대로 일치하지 않는 본문 문자에 대해 참조하는 테이블입니다.
하지만 이러한 테이블 만으로는 정상적으로 동작하는 것을 기대하기 어렵기 때문에 두 번째 방식인 Good Suffix Heuristica 방식으로 테이블을 생성합니다.
이 방식은 KMP 알고리즘과 약간의 유사성이 있습니다.
Suffix, 접미사와 대칭이 되는 것 을 찾아 테이블을 생성하는 방식입니다.
1. Bad Character Heuristica
이 방법은 패턴 문자에 대하여 순서대로 번호를 붙여준다 생각하시면 됩니다.
즉, 비교가 실패하였을 때 만약 그 틀린 본문 문자가 패턴 문자 내에 어딘가에 존재한다면 그곳으로 위치를 변경하는 것입니다.
아래는 패턴 문자열에 각각의 번호를 붙여준 모양입니다.
(얘 시가 순서대로 돼있지만 중복된 문자가 나올 경우 후에 나온 번호가 뒤집어쓰기 때문에 값이 달라집니다. 이해가 안 가시는 분들은 이 글을 읽다 보시면 코드로 구현한 부분에서 좀 더 설명드리겠습니다.)
| pattern string | a | b | c | d |
| special value | 0 | 1 | 2 | 3 |
그렇다면 위의 테이블을 참조하여 다음의 비교를 진행해보겠습니다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| m | a | b | c | a | b | a | b | c | d |
| n | a | b | c | d |
패턴 문자와 본문 문자가 일치하지 않는 부분이 존재합니다.
일치하지 낳는 본문 문자는 a 문자이지만 이 문자를 패턴 문자열 내에서 본 적이 있는 거 같습니다.
그래서 테이블을 확인해 보니 0번에 존재한다는군요.
그럼 다음과 같은 연산을 진행하여 현재의 다음 비교할 위치를 구합니다.
다음 위치 = 본문 문자열 내 현재 INDEX + (패턴 문자열 내의 현재 위치 - 테이블에서 참조한 값)
대입한 결과 : 3 = 0 + (3 +0)
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| m | a | b | c | a | b | a | b | c | d |
| n | a | b | c | d |
그다음에도 일치하지 않는 내용이 발생했습니다.
다음 테이블은 직접 계산해 보고 그려보시는 편이 이해하시는데 도움이 될 거 같습니다.
저희는 첫 번째 방식인 Bad Character Heuristica을 알아봤습니다.
하지만 이와 같은 방식으로만 동작하기에는 정상적으로 동작하지 않는 경우도 발생합니다.
그리고 한 가지 테이블을 더 사용하여 두 테이블 중 더 큰 값으로 넘어간다면 좀 더 반복 횟수를 줄일 수 있을 것입니다.
2. Good Suffix Heuristica
이 방식은 접미사와 같은 문자열이 패턴 문자열 내에 존재하는지 를 검사합니다.
여기서 잠깐 접미사란 문자열 내에서 시작이 어디든 항상 끝까지 나타낸 문자열을 뜻합니다.
아래는 ababcabc에 대한 접미사를 나열한 모습을 보여줍니다.
| ababcabc | 접미사 |
| c | |
| bc | |
| abc | |
| cabc | |
| bcabc | |
| abcabc | |
| babcabc | |
| ababcabc |
그렇다면 접미사와 일치한다는 문자열이란 아래와 같습니다.
| 접미사 | 일치한 문자열 |
| c | ababcabc |
| bc | ababcabc |
| abc | ababcabc |
접미사와 같은 문자열이 무엇인 지 알았으니 아래 테이블은 위의 내용을 테이블로 만든 내용입니다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| pattern | a | b | a | b | c | a | b | c |
| value | 8 | 8 | 5 | 6 | 7 | 8 | 8 | 8 |
접미사와 같았던 문자열이 접미사를 가리키고 있는 것을 확인할 수 있습니다.
하지만 이것만으로 부족합니다. 그 이유는 보이어-무어 알고리즘은 뒤에서부터 비교를 해 나아가기 때문에 저 뒤의 접미사 부분이 바꿉니다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| pattern | a | b | a | b | c | a | b | c |
| value | 8 | 8 | 8 | 8 | 8 | 3 | 8 | 8 |
나머지 값이 패턴 문자열의 길이인 이유는 보이어-무어는 뒤에서부터 비교하기 때문에 틀리면 패턴의 문자열만큼 과감하게 건너뛸 수 있습니다.
위의 테이블은 접미사의 인덱스를 나타냈지만 지금 테이블은 다음 인덱스를 얼마큼 더해서 시작할지를 알려줍니다.
위와 같은 내용으로 c++ 언어로 구현해 보면서 부족한 설명을 해보겠습니다.
구현
1. Bad Character에 대한 테이블을 정의합니다.
Bad Table 은 위에서 설명한 바로 각 문자에 대해 순서대로 번호를 붙여준다고 했습니다.
const int MAX_SIZE = 256;
vector<int> make_to_bad_character_tb(const string pattern){
const int p_size = pattern.size();
vector<int> bc_tb(MAX_SIZE, p_size);
for(int i = 0; i < p_size; ++i)
bc_tb[(int)pattern[i]] = i;
return bc_tb;
}
이 테이블의 문제점은 중복된 문자가 나올 시 기존의 값을 덮어쓴 다했습니다.
반복문 내용을 보시면 받은 문자를 int형으로 바꾼 위치에 값을 저장하는 모습을 볼 수 있을 것입니다.
2. Good Suffix에 대한 테이블을 만듭니다.
vector<int> make_to_gs_tb(const string pattern){
const int p_size = pattern.size();
int pattern_point = p_size;
int suffix_point = pattern_point + 1;
// 접미사와 동일한 문자열 체크하는 테이블
vector<int> suf_tb(p_size + 1, 0);
suf_tb[pattern_point] = suffix_point;
// 생략할 테이블
vector<int> skip_tb(p_size + 1, 0);
while(pattern_point > 0){
// 접미사가 일치하는 순간 몇개가 일치하는지 카운팅
while(suffix_point <= p_size &&
pattern[pattern_point - 1] != pattern[suffix_point -1]){
if(skip_tb[suffix_point] == 0)
skip_tb[suffix_point] = suffix_point - pattern_point;
suffix_point = suf_tb[suffix_point];
}
// 접미사와 동일한 단어가 접미사인덱스를 가르키도록 설정
suf_tb[--pattern_point] = --suffix_point;
}
...
}
위의 코드는 접미사와 동일해질 때 카운트를 시작하여 그에 맞게 배열에 넣어주는 코드입니다.
코드가 한눈에 안 들어와 저도 많이 보고 또 보았습니다.
접미사와 동일한 문자들이 접미사의 인덱스를 가르치도록 만드는 작업이 이루어지는 작업과 일치한 접미사를 찾았을 때 그 얼마큼 스킵할지 저장합니다.
그러면 아래와 같은 테이블이 만들어집니다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| pattern | a | b | a | b | c | a | b | c | |
| suf_tb | 8 | 8 | 5 | 6 | 7 | 8 | 8 | 8 | 9 |
| skip_tb | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 |
위에서 본 테이블과 많이 비슷해졌습니다.
하지만 아직 생략 테이블은 나머지 문자에 대해서 어떻게 스킵해야 할지 모릅니다.
그렇다면 여기서 한 가지 더 설명드리겠습니다.
suf_tb의 목록을 보시면 일치한 값들이 보입니다. 이 값들은 패턴 문자열의 사이즈와 같으면 그 자릿수만큼 생략이 가능하다는 것입니다. 그리고 이 값은 앞자리부터 채워줍니다.
vector<int> make_to_gs_tb(const string pattern){
const int p_size;
int pattern_point = p_size;
int suffix_point = pattern_point + 1;
// 접미사와 동일한 문자열 체크하는 테이블
vector<int> suf_tb(p_size + 1, 0);
// 생략할 테이블
vector<int> skip_tb(p_size + 1, 0);
...
suffix_point = suf_tb[0];
while(pattern_point < p_size){
if(skip_tb[pattern_point] == 0)
skip_tb[pattern_point] = suffix_point;
if(pattern_point++ == suffix_point)
suffix_point = suf_tb[suffix_point];
}
return skip_tb;
}
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| pattern | a | b | a | b | c | a | b | c | |
| suf_tb | 8 | 8 | 5 | 6 | 7 | 8 | 8 | 8 | 9 |
| skip_tb | 8 | 8 | 8 | 8 | 8 | 3 | 8 | 8 | 0 |
그리고 이렇게 나온 값으로 원하는 문자열 검색을 합니다.
그렇다면 테이블 두 개를 어떠한 방식으로 참조하느냐도 중요합니다.
테이블을 참조하여 가장 큰 값을 택한다 생각하시면 됩니다.
int search(const vector<int> bc_tb, const vector <int> gs_tb,
const string H, const string pattern){
const int h_size = H.size();
const int p_size = pattern.size();
int begin = 0;
if(h_size < p_size) return -1;
while(begin <= h_size - p_size){
int matched = p_size;
while(matched > 0 && pattern[matched - 1] == H[begin + (matched - 1)]){
--matched;
}
if(matched == 0) return begin;
if(bc_table[H[begin + matched]] != p_size){
begin += max(matched - bc_tb[H[begin + matched]],
gs_tb[matched]);
}else{
begin += max(gs_tb[matched], matched);
}
}
return -1;
}
전체 코드
#include <iostream>
#include <vector>
using namespace std;
const int MAX_SIZE = 256;
vector<int> make_to_bad_character_tb(const string pattern)
{
const int p_size = pattern.size();
vector<int> bc_tb(MAX_SIZE, p_size);
for (int i = 0; i < p_size; ++i)
bc_tb[(int)pattern[i]] = i;
return bc_tb;
}
vector<int> make_to_gs_tb(const string pattern)
{
const int p_size = pattern.size();
int pattern_point = p_size;
int suffix_point = pattern_point + 1;
// 접미사와 동일한 문자열 체크하는 테이블
vector<int> suf_tb(p_size + 1, 0);
suf_tb[pattern_point] = suffix_point;
// 생략할 테이블
vector<int> skip_tb(p_size + 1, 0);
while (pattern_point > 0)
{
cout <<'h'<<endl;
// 접미사가 일치하는 순간 몇개가 일치하는지 카운팅
while (suffix_point <= p_size &&
pattern[pattern_point - 1] != pattern[suffix_point - 1])
{
if (skip_tb[suffix_point] == 0)
skip_tb[suffix_point] = suffix_point - pattern_point;
suffix_point = suf_tb[suffix_point];
}
// 접미사와 동일한 단어가 접미사인덱스를 가르키도록 설정
suf_tb[--pattern_point] = --suffix_point;
}
suffix_point = suf_tb[0];
while (pattern_point < p_size)
{
if (skip_tb[pattern_point] == 0)
skip_tb[pattern_point] = suffix_point;
if (pattern_point++ == suffix_point)
suffix_point = suf_tb[suffix_point];
}
for(auto & suf : suf_tb)
cout << suf << ", ";
cout << endl;
for(auto & skip : skip_tb)
cout << skip << ", ";
cout << endl;
return skip_tb;
}
int search(const vector<int> bc_tb, const vector<int> gs_tb,
const string H, const string pattern)
{
const int h_size = H.size();
const int p_size = pattern.size();
int begin = 0;
if (h_size < p_size)
return -1;
while (begin <= h_size - p_size)
{
int matched = p_size;
while (matched > 0 && pattern[matched - 1] == H[begin + (matched - 1)])
{
--matched;
}
if (matched == 0)
return begin;
if (bc_tb[H[begin + matched]] != p_size)
{
begin += max(matched - bc_tb[H[begin + matched]],
gs_tb[matched]);
}
else
{
begin += max(gs_tb[matched], matched);
}
}
return -1;
}
int main()
{
const string h = "abaabaababbabababcabccaabcabcabcbcabcbacba";
const string pattern = "abbab";
const int p_size = pattern.size();
const vector<int> bc_table = make_to_bad_character_tb(pattern);
const vector<int> gs_table = make_to_gs_tb(pattern);
cout << search(bc_table, gs_table, h, pattern) << endl;
return 0;
}
끝맺음
보이어-무어 알고리즘은 타 알고리즘에 비해 저도 이해하는데 상당히 오래 걸렸습니다.
지금도 긴가 민가 하는 부분도 종종 생깁니다.
이렇게 한번 정리를 했어도 저 또한 제 글을 또다시 찾아 읽어보고 좀 더 쉽게 설명할 방안이 없나 생각을 더 해봐야 할거 같습니다.
틀린 부분이 있다면 과감히 지적해주시면 감사하겠습니다.
긴 글 읽어주셔서 감사합니다.

'알고리즘' 카테고리의 다른 글
| [프로그래머스] 단어 변환 - DFS(깊이 탐색) 방식(feat.cpp) (0) | 2020.11.09 |
|---|---|
| [KMP] 카누스 모리스 프렛 알고리즘 (feat.cpp) (0) | 2020.11.04 |
| 트라이 알고리즘이란 ? (feat.cpp) (0) | 2020.11.03 |
| [프로그래머스] 위장 (0) | 2020.11.02 |
| [heap] 힙 이란? (feat.cpp) (0) | 2020.11.01 |
[KMP] 카누스 모리스 프렛 알고리즘 (feat.cpp)

K.M.P 알고리즘 이란?
m이라는 문자열 안에 n라는 문자열이 포함되는지 알고 싶은 경우 제일 먼저 생각나는 방법으로는
완전 탐색(Brute Force) 알고리즘이 먼저 생각날 것입니다.
완전 탐색은 간단한 구현만으로도 정확하게 문자열을 찾아낼 수 있지만 길이가 길어질수록 시간이 오래 걸립니다.
m 문자열 길이에 n 문자열 길이만큼 비교하게 되니 시간 복잡도는 O(mn)이나 나옵니다.
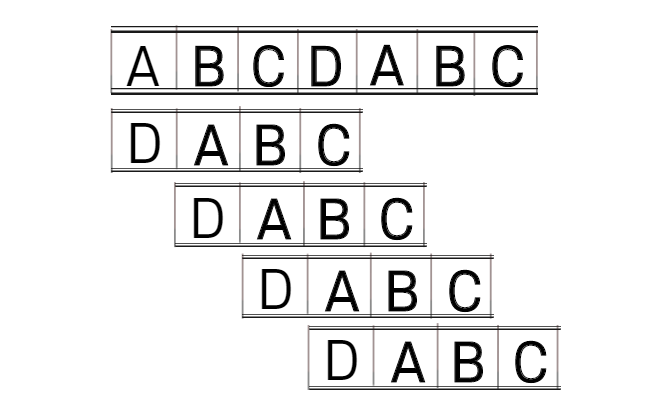
KMP 알고리즘은 저런 비교 결과들을 활용 하여 빠르게 문자열의 어느 INDEX 부터 시작할지를 결정합니다.
아래 표를 보시면 첫 매칭에서 A B C A 까지는 맞지만 나머지가 틀려서 찾지못한 결과입니다.
| INDEX | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| M | A | B | C | A | A | B | C | A | B |
| N | A | B | C | A | B |
만약 완전 탐색으로 탐색을 진행했다면, 아래쳐럼 INDEX 1로 이동하여 비교를 진행할것입니다.
| INDEX | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| M | A | B | C | A | A | B | C | A | B |
| N | A | B | C | A | B |
하지만 KMP은 위에 A B C A 까지 맞은것을 이용하여 A (접두사, 접미사 일치) 한 곳부터 시작을 합니다.
| INDEX | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| M | A | B | C | A | A | B | C | A | B |
| N | A | B | C | A | B |
접두사, 접미사
정보를 활용할 수 있는 방법으로는 접두사 (PREFIX)와 접미사 (SUBFIX)가 같은 지점을 찾습니다.
| ABCAB | 접두사 | 접미사 |
| A | B | |
| AB | AB | |
| ABC | CAB | |
| ABCA | BCAB | |
| ABCAB | ABCAB |
맨 아래 ABCAB는 정보를 찾은 결과이니 제외하고 접두사와 접미사가 같은 부분을 찾아보면 AB 가 있습니다.
이 정보를 가지고 생각해봅시다.
만약에 비교중에 접미사 부분에 포함된 부분이 일치하지만 나머지가 틀렸다면 시작 위치를 접미사로 옮겨도 되지 않을까요?
접미사와 접두사가 같다는 뜻은 시작 위치 값 = 끝나는 위치 값 같다 라는 말입니다.
구현
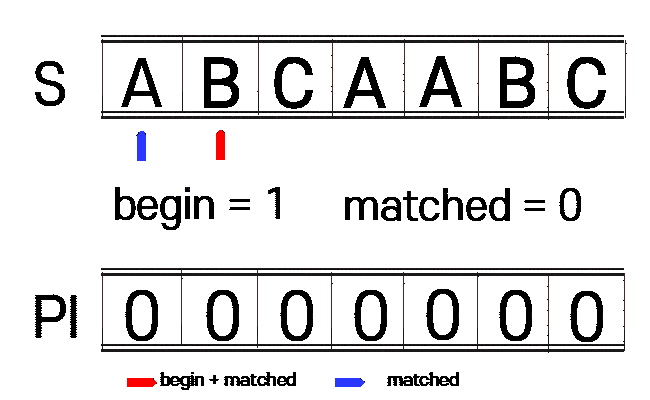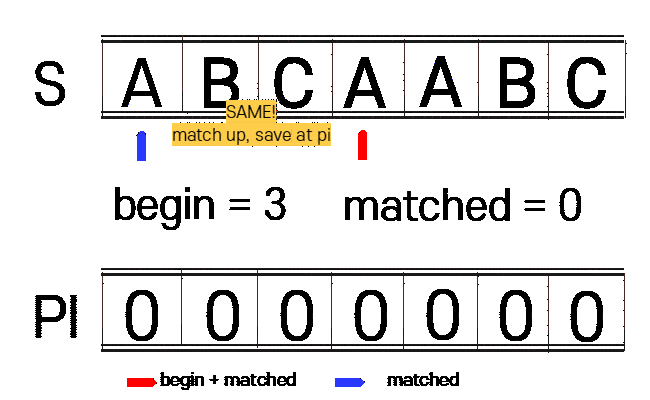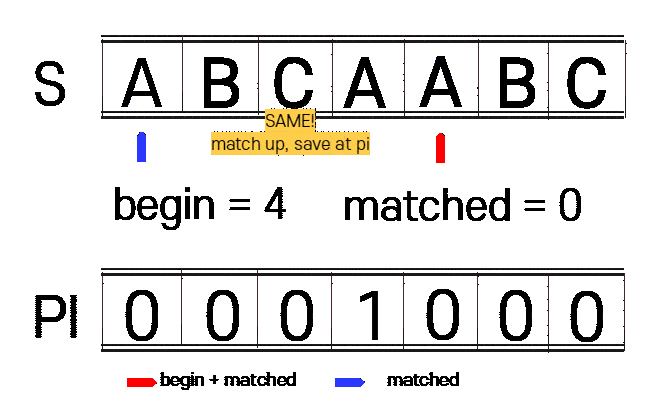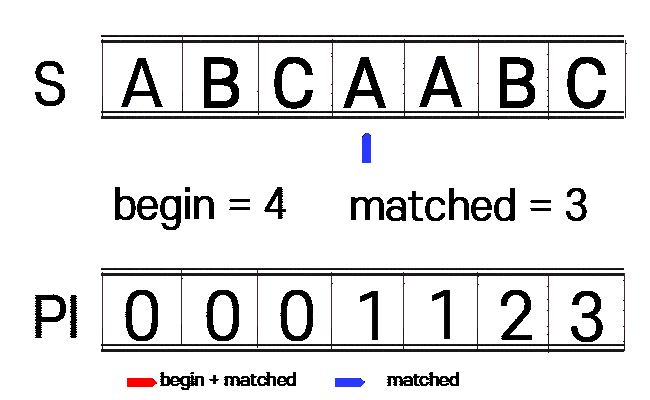
1. n(찾을 문자열)에 대하여 접두사와 접미사가 같은 부분을 찾습니다.(PI 테이블 생성)
begin : 접미사 시작 부분
matched : 접두사 시작 부분
vector<int> get_pi(const string n){
const int n_size = n.size();
int begin = 1, matched = 0;
vector<int> pi(n_size, 0);
while(begin + matched < n_size){
if(n[begin + matched] == n[matched]){
++matched;
pi[begin + matched - 1] = matched;
}else{
if(matched == 0){
++begin;
}else{
begin += matched - pi[matched - 1];
matched = pi[matched - 1];
}
}
}
return pi;
}
2. 문자열을 비교하고 만약 매칭이 되지 않을 시 PI테이블을 보고 시작할 위치를 정합니다.
ret : 찾는 패턴의 시작 위치들을 담고 있는 변수
vector<int> search_to_pettern(const string m, const string n){
vector<int> ret;
const int m_size = m.size();
const int n_size = n.size();
const vector<int> pi = get_pi(n);
int begin = 0, matched = 0;
while(begin + matched < m_size){
if(matched < n_size && m[begin + matched] == n[matched]){
++matched;
if(matched == n_size)
ret.push_back(begin);
}else{
if(matched == 0)
++begin;
else{
begin += matched - pi[matched - 1];
matched = pi[matched - 1];
}
}
}
return ret;
}
전체 코드
#include <iostream>
#include <vector>
using namespace std;
vector<int> get_pi(const string n){
const int n_size = n.size();
int begin = 1, matched = 0;
vector<int> pi(n_size, 0);
while(begin + matched < n_size){
if(n[begin + matched] == n[matched]){
++matched;
pi[begin + matched - 1] = matched;
}else{
if(matched == 0){
++begin;
}else{
begin += matched - pi[matched - 1];
matched = pi[matched - 1];
}
}
}
return pi;
}
vector<int> search_to_pettern(const string m, const string n){
vector<int> ret;
const int m_size = m.size();
const int n_size = n.size();
const vector<int> pi = get_pi(n);
int begin = 0, matched = 0;
while(begin + matched < m_size){
if(matched < n_size && m[begin + matched] == n[matched]){
++matched;
if(matched == n_size)
ret.push_back(begin);
}else{
if(matched == 0)
++begin;
else{
begin += matched - pi[matched - 1];
matched = pi[matched - 1];
}
}
}
return ret;
}
테스트 코드 (필요하신 분만(
int main(){
const string m = "aabaabacabaaaabaabac";
const string n = "aabaabac";
const vector<int> ret = search_to_pettern(m, n);
for(auto & num : ret){
cout << num << endl;
}
return 0;
}

'알고리즘' 카테고리의 다른 글
| [프로그래머스] 단어 변환 - DFS(깊이 탐색) 방식(feat.cpp) (0) | 2020.11.09 |
|---|---|
| [Boyer-Moore] 문자열 탐색 ! 보이어-무어 알고리즘(feat.cpp) (0) | 2020.11.07 |
| 트라이 알고리즘이란 ? (feat.cpp) (0) | 2020.11.03 |
| [프로그래머스] 위장 (0) | 2020.11.02 |
| [heap] 힙 이란? (feat.cpp) (0) | 2020.11.01 |
트라이 알고리즘이란 ? (feat.cpp)

트라이 란?
문자열 탐색을 보다 효율적으로 하기 위해 고안된 알고리즘입니다
단순하게 문자열을 비교해 나가면(brute force) 문자열 길이가 길어질수록 수행 시간이 오래 걸립니다..
반면 트라이 알고리즘은 트리 형태로 문자열을 정리해놓아 탐색 시 빠르게 탐색할 수 있습니다.
단. 트라이 알고리즘은 문자열의 길이가 길어질수록 트리의 깊이도 깊어지므로 공간 복잡도가 안 좋습니다.
아래 사진은 tree라는 문자열을 Insert 하는 과정입니다.
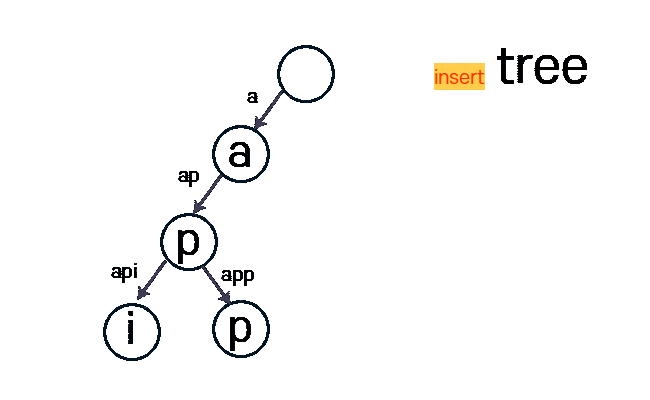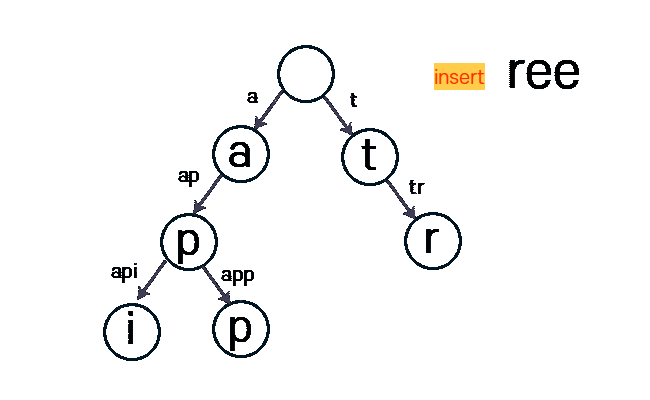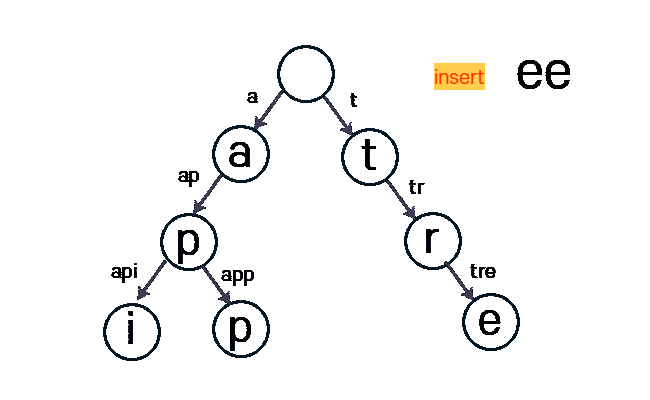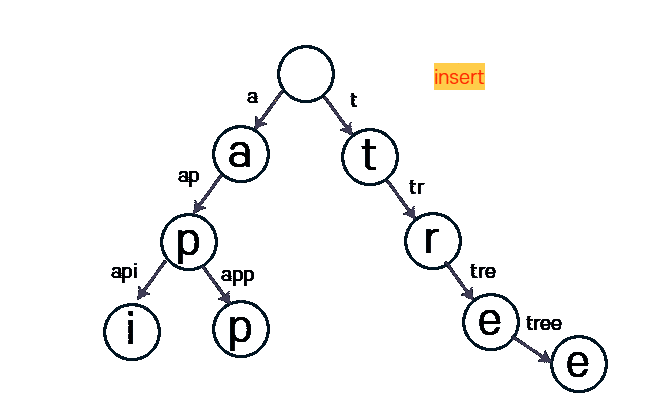
구현 - alpabet 소문자 기준
1. 트라이 클래스 생성
node : 자식 노드를 가리키는 변수(다음 문자를 가리킨다.)
check_end_str : 문자열의 마지막인지 아닌지 체크하는 변수
#define MAX_TRIE_SIZE 26
class Trie{
public :
Trie * node[MAX_TRIE_SIZE];
bool check_end_str;
Trie(){
fill(node, node + MAX_TRIE_SIZE, nullptr);
check_end_str = false;
}
~Trie(){
for(int i = 0; i < MAX_TRIE_SIZE; ++i)
if(node[i] != nullptr)
delete node[i];
}
...
};2. INSERT()
위에서 노드를 보면 26개의 배열로 만들어졌습니다.(알파벳 개수는 26개)
즉, a문자는 node [0], b문자는 node [1]... z문자는 node [25]에 값을 할당해 주기 위함입니다.
그러기 위해서는 알파벳을 노드의 인덱스로 바꾸어 주어야 합니다.
class Trie{
...
int translate_index(const char c){
return c - 'a';
}
...
};
입력받은 문자가 마지막('\0') 일 시 check_end_str을 true 바꾸어 마지막임을 표시합니다.
마지막 문자에 도달할 때까지 노드를 만들거나 기존 노드를 타고 이동합니다.
class Trie{
...
void insert(const char * str){
if(*str == '\0'){
check_end_str = true;
}else{
const int index = translate_index(*str);
if(node[index] == nullptr)
node[index] = new Trie();
node[index]->insert(str + 1);
}
}
...
}
2. find()
트라이 탐색은 INSERT와 다른 점은 반환하는 값이 있다는 것뿐입니다.
마지막 문자열까지 도달했을 경우 문자열을 찾은 것이니 true을 리턴,
만약 마지막 문자열이 아니지만 해당 노드가 비어있다면 false를 리턴하도록 하겠습니다.
class Trie{
...
bool find(const char * str){
if(*str == '\0')
return true;
const int index = translate_index(*str);
if(node[index] == nullptr)
return false;
node[index]->find(str + 1);
}
...
}
전체 코드
#include <iostream>
#include <algorithm>
#define MAX_TRIE_SIZE 26
using namespace std;
class Trie{
public :
Trie * node[MAX_TRIE_SIZE];
bool check_end_str;
Trie(){
fill(node, node + MAX_TRIE_SIZE, nullptr);
check_end_str = false;
}
~Trie(){
for(int i = 0; i < MAX_TRIE_SIZE; ++i)
if(node[i] != nullptr)
delete node[i];
}
int translate_index(const char c){
return c - 'a';
}
void insert(const char * str){
if(*str == '\0'){
check_end_str = true;
}else{
const int index = translate_index(*str);
if(node[index] == nullptr)
node[index] = new Trie();
node[index]->insert(str + 1);
}
}
bool find(const char * str){
if(*str == '\0')
return true;
const int index = translate_index(*str);
if(node[index] == nullptr)
return false;
node[index]->find(str + 1);
}
};
테스트 코드 (필요하신 분만)
words : trie에 저장할 문자열 목록
find_words : 탐색할 문자열 목록
int main(){
Trie * trie = new Trie();
const vector<string> words = {
"apple", "tree", "word", "fire", "egg", "people", "number",
"py", "google", "naver", "daum", "tistory"
};
const vector<string> find_words = {
"apple", "tr", "google", "go", "whole", "find", "num",
"good", "job", "peo", "never", "naver", "py", "pi"
};
// insert
for(auto & word : words){
trie->insert(word.c_str());
}
for(auto & find_word : find_words){
cout << find_word;
if(trie->find(find_word.c_str()))
cout << " is!!!";
else
cout << " isn't...";
cout << endl;
}
return 0;
}

'알고리즘' 카테고리의 다른 글
| [Boyer-Moore] 문자열 탐색 ! 보이어-무어 알고리즘(feat.cpp) (0) | 2020.11.07 |
|---|---|
| [KMP] 카누스 모리스 프렛 알고리즘 (feat.cpp) (0) | 2020.11.04 |
| [프로그래머스] 위장 (0) | 2020.11.02 |
| [heap] 힙 이란? (feat.cpp) (0) | 2020.11.01 |
| [프로그래머스] 가장 큰 수 (0) | 2020.10.30 |
[프로그래머스] 위장

문제 내용
문제 설명
스파이들은 매일 다른 옷을 조합하여 입어 자신을 위장합니다.
예를 들어 스파이가 가진 옷이 아래와 같고 오늘 스파이가 동그란 안경, 긴 코트, 파란색 티셔츠를 입었다면 다음날은 청바지를 추가로 입거나 동그란 안경 대신 검정 선글라스를 착용하거나 해야 합니다.
| 종류 | 이름 |
| 얼굴 | 동그란 안경, 검정 선글라스 |
| 상의 | 파란색 티셔츠 |
| 하의 | 청바지 |
| 겉옷 | 긴 코트 |
스파이가 가진 의상들이 담긴 2차원 배열 clothes가 주어질 때 서로 다른 옷의 조합의 수를 return 하도록 solution 함수를 작성해주세요.
제한사항
-
clothes의 각 행은 [의상의 이름, 의상의 종류]로 이루어져 있습니다.
-
스파이가 가진 의상의 수는 1개 이상 30개 이하입니다.
-
같은 이름을 가진 의상은 존재하지 않습니다.
-
clothes의 모든 원소는 문자열로 이루어져 있습니다.
-
모든 문자열의 길이는 1 이상 20 이하인 자연수이고 알파벳 소문자 또는 '_' 로만 이루어져 있습니다.
-
스파이는 하루에 최소 한 개의 의상은 입습니다.
입출력 예
| clothes | return |
| [[yellow_hat, headgear], [blue_sunglasses, eyewear], [green_turban, headgear]] | 5 |
| [[crow_mask, face], [blue_sunglasses, face], [smoky_makeup, face]] | 3 |
나의 생각
1. 어떻게 풀까?
부위 별 옷의 개수를 정리합니다.
answer : 반환할 변수
m : 옷의 종류를 key값으로 개수를 카운팅 할 변수
#include <unordered_map>
int solution(vector<vector<string>> clothes){
int answer = 1;
unordered_map <string, int> m;
for(int i = 0; i < clothes.size(); ++i){
m[clothes[i][1]]++;
}
}
2. 종류 별로 정리했으면 경우의 수를 어떻게 구할까?
만약 3가지의 옷의 종류(얼굴, 상의, 하의)가 있다면 그 3가지 옷으로 입을 수 있는 경우의 수를 구하는 방법은
아래와 같을 것입니다.
(얼굴 옷의 개수) x (상의 옷의 개수) 개수) x (하의 옷의 개수)
하지만 이번 문제는 각각의 종류의 옷을 안 입는 경우도 포함되어 있습니다.
그렇다면 각 옷의 개수에 1 (옷을 입지 않는 경우)을/를 더해줍니다.
(얼굴 옷의 개수 + 1) x (상의 옷의 개수 + 1) x (하의 옷의 개수 + 1)
그 결과 세 종류의 옷을 다 안 입는 경우도 그 값에 포함되어 결괏값이 나옵니다.
즉, 아예 안 입는 경우를 저 식에서 빼줍니다.
((얼굴 옷의 개수 + 1) x (상의 옷의 개수 + 1) x (하의 옷의 개수 + 1)) - 1
int solution(vector<vector<string>> clothes){
...
for(auto & pair : m)
answer *= (pair.second +1);
return answer - 1;
}
전체 코드
#include <string>
#include <vector>
#include <unordered_map>
using namespace std;
int solution(vector<vector<string>> clothes) {
int answer = 1;
unordered_map <string, int> m;
for(int i = 0; i < clothes.size(); ++i){
m[clothes[i][1]]++;
}
for(auto & pair : m){
answer *= (pair.second + 1);
}
return answer-1;
}
테스트 코드 (필요하신 분만)
int main(){
const vector<vector<vector<string>>> testcases = {
{
{"yellow_hat", "headgear"},
{"blue_sunglasses", "eyewear"},
{"green_turban", "headgear"}
},
{
{"crow_mask", "face"},
{"blue_sunglasses", "face"},
{"smoky_makeup", "face"}
}
};
for(auto & testcase : testcases){
const int ret = solution(testcase);
cout << ret << endl;
}
return 0;
}
'알고리즘' 카테고리의 다른 글
| [KMP] 카누스 모리스 프렛 알고리즘 (feat.cpp) (0) | 2020.11.04 |
|---|---|
| 트라이 알고리즘이란 ? (feat.cpp) (0) | 2020.11.03 |
| [heap] 힙 이란? (feat.cpp) (0) | 2020.11.01 |
| [프로그래머스] 가장 큰 수 (0) | 2020.10.30 |
| [프로그래머스] 괄호 변환 (0) | 2020.10.29 |
[heap] 힙 이란? (feat.cpp)

힙 이란?
완전 이진트리로 구현되어 있으며 속성에 따라 부모 노드에 큰 값, 작은 값 둘 중 하나가 올 수 있습니다.
최대 힙 : 자식 노드보다 부모 노드의 값이 큰 힙을 뜻 합니다.
최소 힙 : 자식 노드보다 부모 노드의 값이 작은 힙을 뜻 합니다.

힙은 반환 시 최대 값 또는 최소 값을 반환합니다.
즉 위의 트리에서 루트 노드(최상위 노드)가 반환 후 재 정렬하여 루트 노드에 최대 값 또는 최소 값을 배치시킵니다.
구현 (최대 힙) - 배열
1. PUSH()
데이터를 힙에 저장하는 작업입니다.
트리를 배열로 생각해 봅니다.
완전 이진트리는 부모 노드 아래에 자식 노드 두 개가 있는 구조입니다.
즉, 자식 / 2의 값이 부모 노드의 인덱스가 됩니다.
void push(int data){
heap[++index] = data;
int child = index;
int parent = child / 2;
...
}
데이터를 저장하기만 하고 끝내면 힙이 되지 않습니다.
최대 힙을 구현하는 것이기 때문에 들어온 값과 상위 노드 값들과 비교하며 정렬을 해줍니다.
정렬 방식은 부모 노드와 자식 노드를 비교하여 자식 노드가 더 클 시 자리를 바꿔주는 작업을 반복하며 루트 노드까지 반복하여 비교해갑니다.
void push(int data){
...
while(child > 1 && heap[child] > heap[parent]){
swap(heap[parent], heap[child]);
// 노드를 타고 올라간다.
child = parent;
parent = child / 2;
}
}
2. POP()
데이터를 꺼내는 작업입니다. (루트 노드 출력)
루트 노드 값을 지우는 방법은 루트 노드 값과 Index에 위치한 값과 자리를 변경합니다.
그 후 index에 값을 0으로 변경합니다.
int pop(){
// 루트 노드값 저장
int ret = heap[1];
// 루트 노드 값 삭제
swap(heap[1], heap[index]);
heap[index] = 0;
--index;
...
return ret;
}
pop() 작업도 push() 작업과 동일하게 재 정렬을 해서 루트 노드에 최대 값이 오도록 해줍니다.
여기서 생각해봐야 할 것은 자식 노드는 두 개입니다.
그렇다면 자식 노드가 두 개인 경우 자식 노드 안의 값이 더 큰 쪽으로 child 값을 지정해 줍니다.
어느 자식의 길로 갈지 정해준다 생각하면 됩니다.
int pop(){
...
int parent = 1;
int child = parent * 2;
// 자식 노드가 2개 라면 (child : 첫번째 자식, child + 1 : 두번째 자식)
if(child + 1 <= index)
child = heap[child] > heap[child + 1] ? child : child + 1;
...
}
어느 자식 쪽으로 갈지 정했으면 현재 값이 들어있는 노드(index)까지 부모와 자식을 비교해서 자식이 크면 부모 위치로 변경해주는 작업을 반복해줍니다.
int pop(){
...
while(child <= index && heap[parent] < heap[child]){
swap(heap[parent], heap[child]);
parent = child;
child = parent * 2;
if(child + 1 <= index)
child = heap[child] > heap[child + 1] ? child : child + 1;
}
...
}
전체 코드
#include <iostream>
#define MAX_SIZE 256
using namespace std;
int heap[MAX_SIZE];
int index = 0;
void swap(int & a, int & b){
int tmp = a;
a = b;
b = tmp;
}
void push(int data){
heap[++index] = data;
int child = index;
int parent = child / 2;
while(child > 1 && heap[parent] < heap[child]){
swap(heap[parent], heap[child]);
child = parent;
parent = child / 2;
}
}
int pop(){
int ret = heap[1];
swap(heap[1], heap[index]);
heap[index--] = 0;
int parent = 1;
int child = parent * 2;
if(child + 1 <= index){
child = (heap[child] > heap[child + 1]) ? child : child + 1;
}
while(child <= index && heap[parent] < heap[child]){
swap(heap[parent], heap[child]);
parent = child;
child = parent * 2;
if(child + 1 <= index){
child = (heap[child] > heap[child + 1]) ? child : child + 1;
}
}
return ret;
}
테스트 코드 (필요하신 분만)
1 : push() 작업
2 : pop() 작업
3 : 현재 배열 안에 상태를 확인할 수 있습니다.
int main()
{
while (true)
{
int choice = 0;
int push_data = 0;
cout << "input : ";
cin >> choice;
switch (choice)
{
case 1:
cout << "push : ";
cin >> push_data;
push(push_data);
break;
case 2:
cout << pop() << endl;
break;
case 3:
for (int i = 1; i < MAX_HEAP_SIZE; ++i)
{
if (heap[i] == 0)
break;
cout << heap[i] << ", ";
}
cout << endl;
cout << "================================" << endl;
break;
default:
return 0;
}
}
return 0;
}

'알고리즘' 카테고리의 다른 글
| 트라이 알고리즘이란 ? (feat.cpp) (0) | 2020.11.03 |
|---|---|
| [프로그래머스] 위장 (0) | 2020.11.02 |
| [프로그래머스] 가장 큰 수 (0) | 2020.10.30 |
| [프로그래머스] 괄호 변환 (0) | 2020.10.29 |
| [프로그래머스] 소수 찾기 (0) | 2020.10.28 |
[프로그래머스] 가장 큰 수

문제 내용
문제 설명
0 또는 양의 정수가 주어졌을 때, 정수를 이어 붙여 만들 수 있는 가장 큰 수를 알아내 주세요.
예를 들어, 주어진 정수가 [6, 10, 2]라면 [6102, 6210, 1062, 1026, 2610, 2106]를 만들 수 있고, 이중 가장 큰 수는 6210입니다.
0 또는 양의 정수가 담긴 배열 numbers가 매개변수로 주어질 때, 순서를 재배치하여 만들 수 있는 가장 큰 수를 문자열로 바꾸어 return 하도록 solution 함수를 작성해주세요.
제한 사항
- numbers의 길이는 1 이상 100,000 이하입니다.
- numbers의 원소는 0 이상 1,000 이하입니다.
- 정답이 너무 클 수 있으니 문자열로 바꾸어 return 합니다.
입출력 예
| numbers | return |
| [6, 10, 2] | "6210" |
| [3, 30, 34, 5, 9] | "9534330" |
나의 생각
1. 어떻게 풀까?
그리디 알고리즘을 사용합니다.
여기서 잠깐!! 그리디 알고리즘이란?
욕심쟁이 알고리즘으로 제일 큰 것부터 우선으로 택하는 알고리즘을 말합니다.
2. 그리디 알고리즘이 잘 작동할 것인가?
그냥 큰 수 순서대로 정렬을 숫자를 만들게 될 시 제대로 된 답이 나오지 않습니다.
위의 케이스를 예를 들어 6, 10이라는 숫자를 큰 순서대로 놓을 시 106(10, 6)이라는 숫자가 됩니다.
하지만 610(6, 10)이라는 순서가 더 큰 숫자이지요.
그러므로 저희는 두 문자열을 순서대로 합친 것과, 반대로 합친 것 중에 큰 수를 택해주면 되는 것입니다.
bool compare_big_number(int a, int b){
const string A = to_string(a);
const string B = to_string(b);
// 순서대로 합 친 수와 반대로 합 친 수 비교
return A + B > B + A;
}위 함수를 sort() 함수와 같이 사용하면 위 함수의 결과를 토대로 정렬이 완성됩니다.
string solution(vector<int> numbers){
...
sort(numbers.begin(), numbers.end(), compare_big_number);
...
}
3. 예외는 존재하지 않을까?
이제 정렬도 되었으니 순서대로 이어 붙이면 가장 큰 수가 완성이 됩니다.
하지만 예외가 존재합니다.
만약에 {0, 0, 0} 테스트 케이스가 온다면 결괏값은 000이라는 값이 출력될 것입니다.
그러므로 아래 식을 통하여 예외를 처리해줍니다.
string solution(vector<int> numbers){
...
// 만약 처음 숫자가 0 일 경우
if(numbers.at(0) == 0) return "0";
...
}(0이 제일 처음 나오면서 큰 수 일 경우는 0으로만 이루어진 테스트 케이스 바께 없습니다.)
전체 코드
bool compare_sum_number(int a, int b){
const string A = to_string(a);
const string B = to_string(b);
return A + B > B + A;
}
string solution(vector<int> numbers) {
string answer = "";
sort(numbers.begin(), numbers.end(), compare_sum_number);
if(numbers.at(0) == 0) return "0";
for(auto number : numbers)
answer += to_string(number);
return answer;
}
테스트 코드 (필요하신 분만)
int main(){int main(){
const vector<vector<int>> numbers_testcases = {
{6, 10, 2},
{3, 30, 34, 5, 9},
{0, 0}
};
for(auto numbers : numbers_testcases){
const string ret = solution(numbers);
cout << ret << endl;
}
return 0;
}
'알고리즘' 카테고리의 다른 글
| [프로그래머스] 위장 (0) | 2020.11.02 |
|---|---|
| [heap] 힙 이란? (feat.cpp) (0) | 2020.11.01 |
| [프로그래머스] 괄호 변환 (0) | 2020.10.29 |
| [프로그래머스] 소수 찾기 (0) | 2020.10.28 |
| 에라토스테네스의 체란? (feat.cpp 구현) (0) | 2020.10.28 |
[프로그래머스] 괄호 변환

문제 내용
문제 설명
카카오에 신입 개발자로 입사한 콘은 선배 개발자로부터 개발 역량 강화를 위해 다른 개발자가 작성한 소스 코드를 분석하여 문제점을 발견하고 수정하라는 업무 과제를 받았습니다. 소스를 컴파일하여 로그를 보니 대부분 소스 코드 내 작성된 괄호가 개수는 맞지만 짝이 맞지 않은 형태로 작성되어 오류가 나는 것을 알게 되었습니다.
수정해야 할 소스 파일이 너무 많아서 고민하던 콘은 소스 코드에 작성된 모든 괄호를 뽑아서 올바른 순서대로 배치된 괄호 문자열을 알려주는 프로그램을 다음과 같이 개발하려고 합니다.
용어의 정의
'('와')' 로만 이루어진 문자열이 있을 경우, '('의 개수와 ')'의 개수가 같다면 이를 균형 잡힌 괄호 문자열이라고 부릅니다.
그리고 여기에 '('와 ')'의 괄호의 짝도 모두 맞을 경우에는 이를 올바른 괄호 문자열이라고 부릅니다.
예를 들어, "(()))("와 같은 문자열은 균형 잡힌 괄호 문자열이지만 올바른 괄호 문자열은 아닙니다.
반면에 "(())()"와 같은 문자열은 균형 잡힌 괄호 문자열 이면서 동시에 올바른 괄호 문자열입니다.
'('와 ')' 로만 이루어진 문자열 w가 균형 잡힌 괄호 문자열이라면 다음과 같은 과정을 통해 올바른 괄호 문자열로 변환할 수 있습니다.
ex)
1. 입력이 빈 문자열인 경우, 빈 문자열을 반환합니다.
2. 문자열 w를 두 "균형 잡힌 괄호 문자열" u, v로 분리합니다. 단, u는 "균형 잡힌 괄호 문자열"로 더 이상 분리할 수 없어야 하며, v는 빈 문자열이 될 수 있습니다.
3. 문자열 u가 "올바른 괄호 문자열"이라면 문자열 v에 대해 1단계부터 다시 수행합니다.
3-1. 수행한 결과 문자열을 u에 이어 붙인 후 반환합니다.
4. 문자열 u가 "올바른 괄호 문자열"이 아니라면 아래 과정을 수행합니다.
4-1. 빈 문자열에 첫 번째 문자로 '('를 붙입니다.
4-2. 문자열 v에 대해 1단계부터 재귀적으로 수행한 결과 문자열을 이어 붙입니다.
4-3. ')'를 다시 붙입니다.
4-4. u의 첫 번째와 마지막 문자를 제거하고, 나머지 문자열의 괄호 방향을 뒤집어서 뒤에 붙입니다. 4-5. 생성된 문자 열을 반환합니다.
입출력 예
| p | result |
| "(()())()" | "(()())()" |
| ")(" | "()" |
| "()))((()" | "()(())()" |
나의 생각
1. 어떻게 풀까?
예시로 주어진 내용 그대로 프로그램을 제작해봅니다.
노란색 밑줄을 조건으로 분기가 일어납니다.("올바른 괄호 문자열" 인지 검사)

bool checked_bracket(string p){
stack <char> st;
const int p_size = p.size();
for(int i = 0; i < p_size; ++i){
if(p.substr(i, 1) == ")"){
if(st.empty()) return false;
st.pop();
}else{
st.push(p[i]);
}
}
if(!st.empty()) return false;
return true;
}
2. 이것을 이용해서 어떤 식으로 문제를 풀까?
문자열 u가 "올바른 괄호 문자열"이라면 문자열 v에 대해 1단계부터 다시 수행합니다.
이 글을 위 함수에 대입해서 얘기하자면 checked_bracket(u) 함수 결과가 true 면 문자열 v로 처음부터 시작합니다.
즉, u는 올바른 문자열이기 때문에 그대로 붙여주고 v에 대해서만 처음부터 검사를 시작합니다.
string solution(string p){
...
if(checked_bracket(u)){
answer += u;
return answer += solution(v);
}
...
}
또 다른 조건, 문자열 u가 "올바른 괄호 문자열"이 아니라면 아래 과정을 수행합니다.
이 조건도 대입해서 바꿔준다면 위의 조건의 else 문이 됩니다.
3. 그러면 else문 내용은?
먼가 길게 적혀있어서 어렵게 느껴졌던 부분이 있습니다.
하지만 잘 읽어보면 전체적인 내용은 이와 같습니다.
1. u의 첫 번째 마지막 문자 제거
2. 제거된 문자열 뒤집기
3. "(" + solution(v) + ")" + 제거된 문자열
string solution(string p){
...
else{
// u의 앞, 뒤 문자열 제거
string word = u.substr(1, u.size() - 2);
// 제거 된 문자열 뒤집기.
for(int i = 0; i < word.size(); ++i){
if(word.substr(i, 1) == ")"){
word.replace(i, 1, "(");
}else{
word.replace(i, 1, ")");
}
}
return answer += "(" + solution(v) + ")" + word;
}
...
}전체 코드
#include <string>
#include <vector>
#include <stack>
using namespace std;
bool checked_bracket(string p){
stack <char> st;
const int p_size = p.size();
for(int i = 0; i < p_size; ++i){
if(p.substr(i, 1) == ")"){
if(st.empty()) return false;
st.pop();
}else{
st.push(p[i]);
}
}
if(!st.empty()) return false;
return true;
}
string solution(string p) {
if(checked_bracket(p)) return p;
string answer = "";
string u = "", v = "";
int left = 0, right = 0;
const int p_size = p.size();
// 좌우 문자열이 균형잡힌 문자열인 경우 breakl
for(int i = 0; i < p_size; ++i){
if(p.substr(i , 1) == ")"){
++left;
}else{
++right;
}
u += p.substr(i, 1);
if(left == right){
v += p.substr(i + 1);
break;
}
}
if(checked_bracket(u)){
answer += u;
return answer += solution(v);
}else{
string word = u.substr(1, u.size() - 2);
for(int i = 0; i < word.size(); ++i){
if(word.substr(i, 1) == ")"){
word.replace(i, 1, "(");
}else{
word.replace(i, 1, ")");
}
}
return answer += "(" + solution(v) + ")" + word;
}
return answer;
}
테스트 코드 (필요하신 분만)
int main(){
vector <string> p_cases = {
"(()())()", ")(", "()))((()"
};
for(int i = 0; i < p_cases.size(); ++i){
const string ret = solution(p_cases[i]);
cout << ret << endl;
}
return 0;
}
'알고리즘' 카테고리의 다른 글
| [프로그래머스] 위장 (0) | 2020.11.02 |
|---|---|
| [heap] 힙 이란? (feat.cpp) (0) | 2020.11.01 |
| [프로그래머스] 가장 큰 수 (0) | 2020.10.30 |
| [프로그래머스] 소수 찾기 (0) | 2020.10.28 |
| 에라토스테네스의 체란? (feat.cpp 구현) (0) | 2020.10.28 |

