[기초 강의] 자바스크립트편 1장 - 변 수

안녕하세요.
이번에 소개할 내용은
어느 프로그래밍 언어든 가장 많이 사용되는 "변수"입니다.
변수 란?
변수는 간단하게 말하면"상자"라고 생각하시면 됩니다.
물건을 보관하고 정리하실 때 다들 상자 하나에 넣어두시죠?
또 친구에게 택배를 보낼 때 또한 상자에 보내죠?
프로그래밍에서의 변수도 이와 같은 역할을 합니다.
var box = 1;

box라는 상자(변수)에 1을 넣어놓은 모습입니다.
변수의 타입
자바스크립트에서 타입은 총 세 가지가 있으며
이 세 가지는 두 분류로 나눌 수 있습니다.
var, let과 const입니다.
var와 let 변수는 값이 언제는 변할 수 있는 반면에
const변수는 한 번 값을 할당하면 바꿀 수 없어요.
비유를 하자면 var, let은 상자에 물건을 넣고 포장을 안 한 상태이고,
const는 상자에 물건을 넣고 내용을 바꿀 수 없도록 포장을 한 상태입니다.
(var와 let의 차이점은 자바스크립트의 호이 스팅 관련 강의에서 설명드리겠습니다.)
var num1 = 1;
let num2 = 2;
const num3 = 3;
// 출력
console.log(num1, num2, num3);
num1 = 2;
num2 = 3;
num3 = 4; //error
console.log(num1, num2, num3);

똑똑하신 여러분들이라면 위의 선언에서 왜 에러가 나는지 알겠지요?
또한, 코드에서 보면
변수는 선언할 때 한 번만 앞에 타입을 선언해주면 이후에는 선언을 안 해주셔도 됩니다.
(console.log(); 함수는 그냥 출력해주는 함수라고만 알고 있으면 됩니다. 자주 쓰니 기억해주세요)
변수 이름의 조건
변수 이름은 아무 이름이나 막 지으시면 안 됩니다.
첫째, 변수 이름은 영문자(대, 소문자), 숫자, 언더바(_)로만 구성이 됩니다.

(사실, 한국어로 변수 이름을 지어도 실행은 되지만 가급적 영어를 씁시다...)
둘째, 변수 이름은 숫자로 시작하면 안 됩니다.
셋째, 변수 이름에는 공백이 들어갈 수 없습니다.
(공백 대신에 언더바(_)를 사용해주세요.)
넷째, 이미 예약된 예약어들은 변수 이름으로 사용할 수 없습니다.
(if, else, for, while 등등...)
좋은 프로그래머는 변수 이름을 용도에 맞게 짓습니다.
const num = 1;
const name = "coderbee"
const age = 99;
console.log(`나의 번호는 ${1번}이고 나의 이름은 ${coderbee}입니다. 나이는 ${age}입니다.`);
데이터 형에 관하여
지금까지 저희가 변수 안에 넣어본 것은 두 가지 데이터 형뿐입니다.
123 12 234와 같은 숫자(number)
"coderbee"와 같은 문자(string)
이 두 개 말고도
배열(array)과 객체(object),
참과 거짓을 나타내는 불리언(boolean),
마지막으로 함수(function)
이 모든 것이 변수 안에 선언될 수 있습니다.
// number
const num = 1;
// string
const name = "coderbee";
// array
const arr = [];
// object
const obj = {};
// boolean
const b = true;
console.log(typeof num); // number
console.log(typeof name); // string
console.log(typeof arr); // object
console.log(typeof obj); // object
console.log(typeof b); // boolean
typeof는 해당 변수가 가지고 있는 데이터의 데이터 형이 무엇인지 알려줍니다.
근데 자세히 보면 먼가 이상하죠?
array(배열)로 선언한 arr 변수가 실제로 typeof를 찍어보니 object 형으로 나옵니다.
이 부분은 추후 제가 설명드리겠습니다.

일단은 기본기에 집중해 봅시다.
끝맺음
어려운 설명은 빼고 최대한 이제 막 입문하시는 분들 초점으로
설명하다 보니 정말 가벼운 느낌이 된 거 같습니다.
하지만, 저의 생각은 이제 막 입문하시는 분들에게는
어렵게 보다 쉽게 전달하는 게 맞는 부분인 거 같았습니다.

앞으로 더 어려운 부분이 많이 나올 텐데 지금부터 어렵게 공부할 필요는 없잖아요?
오늘 배운 것들 직접 코딩해보시고 모르시는 부분은 언제든 댓글로 남겨주세요.
앞으로도 쉽게 쉽게 알려드리려 노력하겠습니다.
긴 글 읽어주셔서 감사합니다.
'강좌 > JAVASCRIPT' 카테고리의 다른 글
| [기초 강의] 자바스크립트편 0장 - 강의 소개 (0) | 2021.06.13 |
|---|
[기초 강의] 자바스크립트편 0장 - 강의 소개

안녕하세요. Coder BEE입니다.
이번 강의는 자바스크립트입니다.
자바스크립트는 제가 현재 주로 사용하고 있는 언어입니다.
그래서 저도 초심으로 돌아간다는 마음으로 천천히 여러분들께 소개해드리고자 합니다.
소 개
두 가지 질문을 해보겠습니다.
1. 자바스크립트는 자바와 연관성이 깊다.
2. 자바스크립트는 웹에서만 사용되는 언어이다.
두 가지 질문에 대해 답을 내리셨나요?
첫 째, 자바스크립트는 자바와 전혀 연관성이 없습니다.
자바, 현재도 많이 쓰이고 종종 주변에서 듣거나 컴퓨터를 하다 보면 볼 때도 있을 겁니다.
자바스크립트가 세상에 나오기 위해 준비할 때
그때도 자바는 인기 있는 언어였습니다.
그래서 자바스크립트는 인기 있는 언어인 자바의 이름을 따온 겁니다.

"자바스크립트 : 나도 인싸 할래.."
둘째, 자바스크립트가 웹에 친숙한 것은 맞습니다.
하지만 웹에서만 쓸 수 있는 것은 아닙니다.
목 차
1. 변수
2. 조건문
3. 반복문
4. 함수
5. 웹에서의 자바스크립트
끝 맺 음
이번 강의는 기초강의이기에 정말 간단한 것들로 준비해봤습니다.
HTML, CSS강의가 완성된 후
자바스크립트 심화 강의와 따라 하면서 만들어 보기 등 다양한 예제로
여러분들에게 더 많은 것들을 알려드리겠습니다.

잘 부탁드립니다.
'강좌 > JAVASCRIPT' 카테고리의 다른 글
| [기초 강의] 자바스크립트편 1장 - 변 수 (0) | 2021.06.14 |
|---|
[프로그래머스] 자물쇠와 열쇠 - 2020 카카오 공채 (완전탐색

문제 내용
문제 설명
고고학자인 튜브는 고대 유적지에서 보물과 유적이 가득할 것으로 추정되는 비밀의 문을 발견하였습니다. 그런데 문을 열려고 살펴보니 특이한 형태의 자물쇠로 잠겨 있었고 문 앞에는 특이한 형태의 열쇠와 함께 자물쇠를 푸는 방법에 대해 다음과 같이 설명해 주는 종이가 발견되었습니다.
잠겨있는 자물쇠는 격자 한 칸의 크기가 1 x 1인 N x N 크기의 정사각 격자 형태이고 특이한 모양의 열쇠는 M x M 크기인 정사각 격자 형태로 되어 있습니다.
자물쇠에는 홈이 파여 있고 열쇠 또한 홈과 돌기 부분이 있습니다. 열쇠는 회전과 이동이 가능하며 열쇠의 돌기 부분을 자물쇠의 홈 부분에 딱 맞게 채우면 자물쇠가 열리게 되는 구조입니다. 자물쇠 영역을 벗어난 부분에 있는 열쇠의 홈과 돌기는 자물쇠를 여는 데 영향을 주지 않지만, 자물쇠 영역 내에서는 열쇠의 돌기 부분과 자물쇠의 홈 부분이 정확히 일치해야 하며 열쇠의 돌기와 자물쇠의 돌기가 만나서는 안됩니다. 또한 자물쇠의 모든 홈을 채워 비어있는 곳이 없어야 자물쇠를 열 수 있습니다.
열쇠를 나타내는 2차원 배열 key와 자물쇠를 나타내는 2차원 배열 lock이 매개변수로 주어질 때, 열쇠로 자물쇠를 열 수 있으면 true를, 열 수 없으면 false를 return 하도록 solution 함수를 완성해주세요.
제한사항
-
key는 M x M(3 ≤ M ≤ 20, M은 자연수) 크기 2차원 배열입니다.
-
lock은 N x N(3 ≤ N ≤ 20, N은 자연수) 크기 2차원 배열입니다.
-
M은 항상 N 이하입니다.
-
key와 lock의 원소는 0 또는 1로 이루어져 있습니다.
-
0은 홈 부분, 1은 돌기 부분을 나타냅니다.
-
입출력 예
| key | lock | result |
| [[0, 0, 0], [1, 0, 0], [0, 1, 1]] | [[1, 1, 1], [1, 1, 0], [1, 0, 1]] | true |
문제 해석
여러분들은 처음에 이 문제를 보고 어떤 방법으로 풀어야 할지 생각해보시고 제 글을 보고 있을 거라 생각합니다.
저 역시 처음에 깊이/너비 탐색으로 회전, 상, 하, 좌, 우로 이동하는 경우를 탐색을 할까 생각하였습니다.
하지만 key가 lock안에서만 움직이는것도 아니고 어디서 끝을 맺어야 할지 모르므로 이 방법은 아니라고 느꼈습니다.
도저히 방법이 생각이 안 나 다른 분들의 풀이를 보았고 제가 잊지 않기 위해 다시 한전 정리할 겸 여러분들께 알려드립니다.
key는 M x M(3 ≤ M ≤ 20, M은 자연수) 크기 2차원 배열입니다.
lock은 N x N(3 ≤ N ≤ 20, N은 자연수) 크기 2차원 배열입니다.
이 두 글을 보시면 key와 lock 사이즈가 M, N으로 서로 다른 정사각형임을 알 수 있습니다.
그리고 두 번째로 알 수 있는 사실은 사이즈입니다.
사이즈가 중요한 이유는 최대 사이즈가 완전 탐색 기법을 사용하였을 때 시간 안에 수행이 가능한 지를 보셔야 합니다.
최대 사이즈가 20 정도면 충분히 완전 탐색 기법을 사용해도 될 거 같습니다.
그렇다면 이것을 어떻게 서로 비교해 나갈까?입니다.
이것을 회전과, 상, 하, 좌, 우 이동을 한 번에 생각을 하면 머리가 아픕니다.
이것을 쪼개여 상, 하 좌, 우 이동과, 회전으로 나누어 생각해봅니다.
혹시 모눈종이라고 다들 아십니까?
모눈 종이 위에 특정 값을 적어 다른 종이에 비교하면 비치는 것처럼 이것도 이러한 방식을 이용하여 탐색해 보면 어떨까요

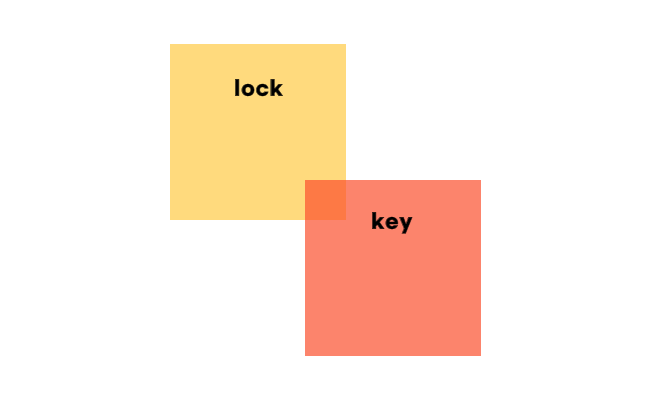
이런 방식으로 배열 자체를 이동하여 비교를 하는 것입니다.
이제 key 배열을 재배치하여 회전시켜 다시 위와 같이 비교해 나아가면 회전과 이동을 다 구현한 모습이 완성됩니다.
구현
위의 그림처럼 모눈종이 방법처럼 비교해 나아가려면 lock의 배열 사이즈를 크게 만들어줘야 할 거 같습니다.
key의 배열은 lock 밖에서도 비교하고 있기 때문입니다.
그럼 얼마큼 lock의 사이즈를 늘려주면 될까?

위 그림을 보시면 처음 비교를 시작하는 모습입니다.
배열의 길이가 기존 lock 배열 길이에서 key 배열 길이 - 1만큼 더 앞으로 생겼습니다.
또한 이 길이는 반대쪽까지 비교해야 하니 반대쪽도 key 배열 길이 - 1만큼 더 추가해 줘야 합니다.
board = lock의 길이 + ( key의 길이 - 1 ) * 2
이제 어느 정도 배열을 만들어야 하는지 알았으니 만들어보겠습니다.
void make_board(vector<vector<int>> &board, const vector<vector<int>> lock, const int key_size)
{
const int board_size = board.size();
for (int i = key_size - 1; i <= board_size - key_size; ++i)
{
for (int j = key_size - 1; j <= board_size - key_size; ++j)
board[i][j] = lock[i - key_size + 1][j - key_size + 1];
}
}
bool solution(vector<vector<int>> key, vector<vector<int>> lock)
{
int answer = false;
const int lock_size = lock.size();
const int key_size = key.size();
const int board_size = lock_size + (key_size - 1) * 2;
vector<vector<int>> board(board_size, vector<int>(board_size, 0));
make_board(board, lock, key_size);
...
}
위 내용을 지나면 아래와 같은 큰 보드 판이 만들어집니다.(문제 예시로 예를 들겠습니다.)
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
외와 같은 그림을 이제 회전과 이동을 하면서 비교하면 이번 문제는 해결될 거 같습니다.
비교 방식은 회전한 key배열을 모든 이동에 비교해 본 후 풀리나 안 풀리나 확인하는 방식입니다.
즉, 회전을 담당하는 반복분 안에 이동을 담당하는 반복문이 있는 그림입니다.
그리고 회전은 90도 회전 기준으로 총 360도가 한 바퀴이니 4번만 돌려주면 모든 방향으로 탐색이 가능합니다.
bool solution(vector<vector<int>> key, vector<vector<int>> lock)
{
...
int rotate = 0;
while (rotate < 4)
{
for (int i = 0; i < board_size - key_size; ++i)
{
for (int j = 0; j < board_size - key_size; ++j)
{
if (insert_key(i, j, board, key))
{
answer = true;
return answer;
}
}
}
rotate_key(key);
++rotate;
}
return answer;
}
위 그림에서 각 시작 값을 insert_key에 넣어 비교하는 중입니다.
여기서 key와 lock은 1이나 0이 저장되었습니다.
그리고 key값과 lock값이 더 해졌을 때 2가 나오면 키와 lock의 위치가 겹친다는 뜻입니다.
또한 0일 경우에는 lock에 값이 정상적으로 들어가지 않아 풀리지 않은 것입니다.
즉, lock의 모든 값이 1로 통일돼야 정상적으로 key의 값이 lock에 들어갔다 할 수 있습니다.
bool insert_key(const int start_y, const int start_x,
vector<vector<int>> board, vector<vector<int>> key)
{
const int board_size = board.size();
const int key_size = key.size();
for (int i = start_y; i < start_y + key_size; ++i)
{
for (int j = start_x; j < start_x + key_size; ++j)
board[i][j] += key[i - start_y][j - start_x];
}
// show_board(board);
for (int i = key_size - 1; i <= board_size - key_size; ++i)
{
for (int j = key_size - 1; j <= board_size - key_size; ++j)
{
const int value = board[i][j];
if (value == 0 || value > 1)
return false;
}
}
return true;
}
주석으로 달아놓은 show_board() 함수는 테스트 코드에 같이 첨부하겠습니다.
show_board() 함수는 board의 변화를 확인할 수 있는 코드입니다.
마지막으로 회전하는 것을 담당하는 rotate_key() 함수입니다.
이 함수는 90도씩 회전하는 함수입니다.
(매개변수로 받을 때 그 안의 값이 변경될 시 '&' 참조자를 사용하여 계산하는 것이 속도면에서도 빠릅니다.)
void rotate_key(vector<vector<int>> &key)
{
const int key_size = key.size();
vector<vector<int>> key_tmp(key_size, vector<int>(key_size, 0));
for (int i = key_size - 1; i >= 0; --i)
{
for (int j = 0; j < key_size; ++j)
{
key_tmp[i][j] = key[key_size - j - 1][i];
}
}
key = key_tmp;
}
전체 코드
#include <iostream>
#include <vector>
using namespace std;
void rotate_key(vector<vector<int>> &key)
{
const int key_size = key.size();
vector<vector<int>> key_tmp(key_size, vector<int>(key_size, 0));
for (int i = key_size - 1; i >= 0; --i)
{
for (int j = 0; j < key_size; ++j)
{
key_tmp[i][j] = key[key_size - j - 1][i];
}
}
key = key_tmp;
}
void make_board(vector<vector<int>> &board, const vector<vector<int>> lock, const int key_size)
{
const int board_size = board.size();
for (int i = key_size - 1; i <= board_size - key_size; ++i)
{
for (int j = key_size - 1; j <= board_size - key_size; ++j)
board[i][j] = lock[i - key_size + 1][j - key_size + 1];
}
}
bool insert_key(const int start_y, const int start_x,
vector<vector<int>> board, vector<vector<int>> key)
{
const int board_size = board.size();
const int key_size = key.size();
for (int i = start_y; i < start_y + key_size; ++i)
{
for (int j = start_x; j < start_x + key_size; ++j)
board[i][j] += key[i - start_y][j - start_x];
}
// show_board(board);
for (int i = key_size - 1; i <= board_size - key_size; ++i)
{
for (int j = key_size - 1; j <= board_size - key_size; ++j)
{
const int value = board[i][j];
if (value == 0 || value > 1)
return false;
}
}
return true;
}
bool solution(vector<vector<int>> key, vector<vector<int>> lock)
{
int answer = false;
const int lock_size = lock.size();
const int key_size = key.size();
const int board_size = lock_size + (key_size - 1) * 2;
vector<vector<int>> board(board_size, vector<int>(board_size, 0));
make_board(board, lock, key_size);
int rotate = 0;
while (rotate < 4)
{
for (int i = 0; i < board_size - key_size; ++i)
{
for (int j = 0; j < board_size - key_size; ++j)
{
if (insert_key(i, j, board, key))
{
answer = true;
return answer;
}
}
}
rotate_key(key);
++rotate;
}
return answer;
}
테스트 코드 (필요하신 분만)
int main()
{
const vector<vector<vector<int>>> key_testcases{
{{0, 0, 0},
{1, 0, 0},
{0, 1, 1}}};
const vector<vector<vector<int>>> lock_testcases{
{{1, 1, 1},
{1, 1, 0},
{1, 0, 1}}};
for (int i = 0; i < key_testcases.size(); ++i)
{
const int ret = solution(key_testcases[i], lock_testcases[i]);
cout << ret << endl;
}
return 0;
}
아래는 보드를 확인해주는 함수입니다.
void show_board(vector<vector<int>> board)
{
const int board_size = board.size();
for (int i = 0; i < board_size; ++i)
{
for (int j = 0; j < board_size; ++j)
{
cout << board[i][j] << " ";
}
cout << endl;
}
}
끝맺음
이번 문제는 저도 상당히 생각을 해보았지만 스스로 풀지는 못하였던 문제입니다.
다시 한번 함수 별로 정리를 하면서 각각이 어떤 의미를 하는지 또한 어떻게 푸는지 알 수 있습니다.
이 문제는 풀이를 보더라도 배열을 구성하는 방법이 수식으로 되어있어 다소 직관적이지 않을 수 있으나 조금만 손으로 적어보시면 금방 깨달으실 수 있을 거라 생각합니다..
저 또한 이해가 안 갈 때마다 종이를 꺼내어 항상 그려보곤 합니다. 하하...

[프로그래머스] 단어 변환 - DFS(깊이 탐색) 방식(feat.cpp)

문제 내용
문제 설명
두 개의 단어 begin, target과 단어의 집합 words가 있습니다. 아래와 같은 규칙을 이용하여 begin에서 target으로 변환하는 가장 짧은 변환 과정을 찾으려고 합니다.
|
1. 한 번에 한 개의 알파벳만 바꿀 수 있습니다. |
예를 들어 begin이 hit, target가 cog, words가 [hot, dot, dog, lot, log, cog]라면 hit-> hot -> dot -> dog -> cog와 같이 4단계를 거쳐 변환할 수 있습니다.
두 개의 단어 begin, target과 단어의 집합 words가 매개변수로 주어질 때, 최소 몇 단계의 과정을 거쳐 begin을 target으로 변환할 수 있는지 return 하도록 solution 함수를 작성해주세요.
제한사항
-
각 단어는 알파벳 소문자로만 이루어져 있습니다.
-
각 단어의 길이는 3 이상 10 이하이며 모든 단어의 길이는 같습니다.
-
words에는 3개 이상 50개 이하의 단어가 있으며 중복되는 단어는 없습니다.
-
begin과 target은 같지 않습니다.
-
변환할 수 없는 경우에는 0을 return 합니다.
입출력 예
| begin | target | words | return |
| hit | cog | [hot, dot, dog, lot, log, cog] | 4 |
| hit | cog | [hot, dot, dog, lot, log] | 0 |
문제 설명
begin을 target으로 바꾸는 방법 중 최소의 비용으로 바꿀 수 있는 방법을 알아내라는 문제입니다.
조건부터 다시 풀어 적어보겠습니다.
첫 번째 조건인 "한 번에 한 개의 알파벳만 바꿀 수 있습니다." 이 말을 다른 말로 하자면 begin의 값과 바뀔 문자가 서로 한 글자만 다르다는 뜻입니다.
그리고 조금 더 생각해 보셔야 할 조건인 두 번째 조건인 "words에 있는 단어로만 변환할 수 있습니다."은 첫 번째 조건과 같이 생각해보자면 "내가 고를 수 있는 words는 한 글자만 다른 words입니다" 이런 식으로 생각할 수 있습니다.
하지만 내가 고를 수 있는 문자가 한 개로 한정되어 있지 않습니다.
위에 예제로 예를 들자면 값이 hit인 begin 변수가 바뀔 수 있는 words는 hot입니다.
그렇다면 hot에서 변할 수 있는 words는 dot와 lot 두 개 나 존재합니다.
이 처럼 값을 선택할 때마다 경우의 수는 한 개가 아니라 여러 개가 나올 수 있습니다.
그리고 그중에서 최소로 변환해야 할 경우를 알아내야 한다는 것입니다.
이렇게 값을 찾아내는 것을 보통 탐색이라고 합니다.
하지만 그냥 탐색만으로는 이전 값들의 경우의 수들도 다 확인하기는 힘듭니다.
하지만 이런 탐색은 가능하지 않을까요?

위 그림은 DFS, 깊이 탐색 방법입니다.
이 방법을 에서 O안에 저장된 값들만 쏙 바꿔 보겠습니다.

깊이 탐색 중 일부를 잘라서 보고 있긴 하지만 이것만 봐도 전체 경우의 수를 모두 탐색할 수 있을 거 같지 않나요?
그럼 어떻게 풀어야 할지 알았으니 하나하나 c++을 사용하여 코드를 만들어 보겠습니다.
구현
첫째로 깊이 탐색을 하는데 생각해야 할 점은 같은 곳을 중복해서 들리면 안 되도록 해줘야 합니다.
그래서 그것을 체크해주는 변수부터 만들어 주어야 됩니다.
answer : 리턴 값 (51로 초기화되어있는 이유는 이 문제의 경우의 수 중 나올 수 없는 값입니다.)
size : words 배열 크기 변수
w_size : 문자열의 길이 변수
int solution(string begin, string target, vector<string> words){
int answer = 51;
const int size = words.size();
const int w_size = words[0].size();
vector<bool> checked(size, false);
...
}저는 항상 이런 식의 탐색을 할 때는 탐색을 완료했다는 checked 나 visited 변수를 만들어 사용합니다.
그럼 깊이 탐색을 위한 변수도 만들었겠다 이제 생각해볼 것은 어떤 words로 시작을 할까입니다.(시작점 정하기)
어떤 것으로 시작하냐에 따라 또 값들이 다 달라질 수 있기 때문입니다.
그렇다면 words의 길이만큼 반복을 하면서 begin문자열과 한 글자만 다른 문자열을 선택하면 되겠습니다.
count : 문자가 서로 다를 경우 카운팅 해주는 변수
DFS : 재귀적으로 깊이 탐색할 함수
track : 재귀 함수를 돌면서 개수를 세어줍니다.
int solution(string begin, string target, vector<string> words){
...
for(int i = 0; i < size; ++i){
int count = 0;
for(int j = 0; j < w_size; ++j)
if(begin[j] != words[i][j])
++count;
if(count == 1){
// 문자 한 개만 다르다면...
checked[i] = true;
int track = 0;
answer = min(answer, DFS(words[i], target,
words, size, w_size,
checked, track) + 1);
checked[i] = false;
}
}
...
}(재귀적으로 돌고 나온 값에 +1을 해준 이유는 처음에 시작할 값을 정할 때 한번 변환했기 때문입니다.)
자, 그러면 이제 깊이 탐색을 위한 시작점을 정하였고, DFS 함수를 통하여 그 시작점에 대해 완전 탐색을 할 수 있게 되었습니다.
그렇다면 이제 깊이 탐색(DFS 함수 내부)을/를 구현하면 되겠군요.
int DFS(const string start, const string target,
const vector<string> words, const int size, const int w_size,
vector<bool> & checked, int track){
if(start == target){
return track;
}
int ret = 51;
for(int i = 0; i < size; ++i){
if(checked[i] == false){
int count = 0;
for(int j = 0; j < w_size; ++j)
if(start[j] != words[i][j])
++count;
if(count == 1){
checked[i] = true;
ret = min(ret, DFS(words[i], target, words, size, w_size, checked, ++track));
--track;
checked[i] = false;
}
}
}
return ret;
}
혹시 이 함수의 구조 중 아까 저희가 만들었던 코드가 비슷해 보이지 않습니까?
그 이유는, 처음 저희가 시작 값을 정할 때와 다음에 어떤 값을 정하는 조건이 같기 때문입니다.
그렇기 때문에 코드가 비슷한 것입니다.
이렇게 재귀 함수가 돌다가 딱 start 문자열과 target 문자열이 같아지는 순간 몇 번째에 문자열이 같아졌는지 반환합니다.
만약에 같아지는 순간이 없다면 (변환되지 않았다면) 반환 값이 51이겠지요?
문제 내용에서 보면 변환이 안될 경우 0을 반환해 달라고 요구 사항이 있었으니 값이 51일 때 0을 반환해주는 코드를 작성하면 되겠군요!
int solution(string begin, string target, vector<string> words){
...
if(answer == 51)
answer = 0;
return answer;
}
전체 코드
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int DFS(const string start, const string target,
const vector<string> words, const int size, const int w_size,
vector<bool> & checked, int track){
if(start == target){
return track;
}
int ret = 51;
for(int i = 0; i < size; ++i){
if(checked[i] == false){
int count = 0;
for(int j = 0; j < w_size; ++j)
if(start[j] != words[i][j])
++count;
if(count == 1){
checked[i] = true;
ret = min(ret, DFS(words[i], target, words, size, w_size, checked, ++track));
--track;
checked[i] = false;
}
}
}
return ret;
}
int solution(string begin, string target, vector<string> words){
int answer = 51;
const int size = words.size();
const int w_size = words[0].size();
vector<bool> checked(size, false);
for(int i = 0; i < size; ++i){
int count = 0;
for(int j = 0; j < w_size; ++j)
if(begin[j] != words[i][j])
++count;
if(count == 1){
// 문자 한 개만 다르다면...
checked[i] = true;
int track = 0;
answer = min(answer, DFS(words[i], target,
words, size, w_size,
checked, track) + 1);
checked[i] = false;
}
}
if(answer == 51)
answer = 0;
return answer;
}
테스트 코드 (필요하신 분만)
int main(){
const vector<string> begin_testcases = {
"hit", "hit"
};
const vector<string> target_testcases = {
"cog", "cog"
};
const vector<vector<string>> words_testcases ={
{"hot", "dot", "dog", "lot", "log", "cog"},
{"hot", "dot", "dog", "lot", "log"}
};
for(int i = 0; i < begin_testcases.size(); ++i){
const int ret = solution(begin_testcases[i], target_testcases[i], words_testcases[i]);
cout << ret << endl;
cout << "===================" << endl;
}
return 0;
}
끝맺음
프로그래머스 문제인 단어 변환을 풀어보면서 깊이 탐색이라는 것을 알아봤습니다.
하지만 이 방법은 하나하나 모든 경우의 수를 살펴보기 때문에 길이가 길어질수록 시간이 오래 걸립니다.
그래도 어느 한 문제를 풀기에는 강력한 알고리즘인 것은 틀림없기에 기억해 두시면 좋을 거 같습니다.
또 제가 푸는 방법이 최고의 방법은 아니기에 항상 많은 지적을 해주시면 감사하겠습니다.

'알고리즘' 카테고리의 다른 글
| [Boyer-Moore] 문자열 탐색 ! 보이어-무어 알고리즘(feat.cpp) (0) | 2020.11.07 |
|---|---|
| [KMP] 카누스 모리스 프렛 알고리즘 (feat.cpp) (0) | 2020.11.04 |
| 트라이 알고리즘이란 ? (feat.cpp) (0) | 2020.11.03 |
| [프로그래머스] 위장 (0) | 2020.11.02 |
| [heap] 힙 이란? (feat.cpp) (0) | 2020.11.01 |
[Boyer-Moore] 문자열 탐색 ! 보이어-무어 알고리즘(feat.cpp)
문자열 탐색
보이어 무어 알고리즘은 KMP 알고리즘과 같이 대표적인 문자열 탐색 알고리즘입니다.
문자열을 탐색할 시 고지식한 알고리즘(완전 탐색 알고리즘)을 사용할 시 상당한 길이가 짧은 문자열일 경우에는 상관없지만 그의 길이가 길어질수록 상당한 시간이 소요됩니다.
그러한 시간 복잡도 문제를 해결하기 위한 대표적인 알고리즘 두 개가 KMP 알고리즘과 이번에 알아볼 보이어-무어 알고리즘입니다.
KMP 알고리즘과 보이어-무어 알고리즘은 보이어-무어 알고리즘은 상당히 비슷한 메커니즘을 갖고 있습니다.
고지식한 알고리즘은 다음 인덱스로 한 칸씩 이동하는 반면 KMP 알고리즘과 보이어-무어 알고리즘은 미리 정의해둔 테이블을 참조하여 다음에 비교할 위치로 건너뛰어 버립니다.
이러한 행위는 반복 횟수를 상당히 줄일 수 있습니다.
그렇다면 보이어-무어 알고리즘은 어떤 방식으로 문자열을 건너뛰게 되는지 이제부터 알아가 보겠습니다.
보이어-무어 알고리즘
기존 고지식한 알고리즘과, KMP 알고리즘 혹은 지금까지 봐왔던 알고리즘들은 대부분 처음부터 비교해 나갈 것입니다.
하지만 보이어-무어 알고리즘은 뒤에서부터 비교해나갑니다.
뒤에서부터 비교를 진행해 나가다 비교 값이 서로 다를 시 테이블을 참조해 나아갑니다.
아래는 보이어-무어 알고리즘으로 비교해 나아가는 이미지입니다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| m | a | b | c | a | b | a | b | c | d |
| n | a | b | c | d |
뒤에서 비교하다 index 3번이 다르다는 것을 확인 후 테이블을 참조합니다.
테이블을 참조 후 다음 비교할 위치로 건너뜁니다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| m | a | b | c | a | b | a | b | c | d |
| n | a | b | c | d |
그다음 값을 보면 index 5, 6번이 다르지만 보이어-무어 알고리즘은 뒤에서부터 비교하므로 테이블 참조 시 index 6번에 대한 값을 참조하여 다음 비교 위치로 넘어갑니다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| m | a | b | c | a | b | a | b | c | d |
| n | a | b | c | d |
총 2번의 이동만으로 원하는 값을 찾아냈습니다.
만약 고지식한 알고리즘이었다면 2번 이동했을 때쯤 index 2번에 n의 문자열이 위치했습니다.
그럼 아까부터 언급하고 계속 참조했던 테이블에 대하여 알아보겠습니다.
생략 테이블
생략 테이블은 제가 설명하기 쉽게 붙인 이름입니다.
패턴 문자열을 찾기 위해 패턴 문자열에 대해 생략 테이블이 2개가 필요합니다.
첫 번째로는 Bad Character Heuristica 방식으로 테이블을 생성합니다.
영어 그대로 일치하지 않는 본문 문자에 대해 참조하는 테이블입니다.
하지만 이러한 테이블 만으로는 정상적으로 동작하는 것을 기대하기 어렵기 때문에 두 번째 방식인 Good Suffix Heuristica 방식으로 테이블을 생성합니다.
이 방식은 KMP 알고리즘과 약간의 유사성이 있습니다.
Suffix, 접미사와 대칭이 되는 것 을 찾아 테이블을 생성하는 방식입니다.
1. Bad Character Heuristica
이 방법은 패턴 문자에 대하여 순서대로 번호를 붙여준다 생각하시면 됩니다.
즉, 비교가 실패하였을 때 만약 그 틀린 본문 문자가 패턴 문자 내에 어딘가에 존재한다면 그곳으로 위치를 변경하는 것입니다.
아래는 패턴 문자열에 각각의 번호를 붙여준 모양입니다.
(얘 시가 순서대로 돼있지만 중복된 문자가 나올 경우 후에 나온 번호가 뒤집어쓰기 때문에 값이 달라집니다. 이해가 안 가시는 분들은 이 글을 읽다 보시면 코드로 구현한 부분에서 좀 더 설명드리겠습니다.)
| pattern string | a | b | c | d |
| special value | 0 | 1 | 2 | 3 |
그렇다면 위의 테이블을 참조하여 다음의 비교를 진행해보겠습니다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| m | a | b | c | a | b | a | b | c | d |
| n | a | b | c | d |
패턴 문자와 본문 문자가 일치하지 않는 부분이 존재합니다.
일치하지 낳는 본문 문자는 a 문자이지만 이 문자를 패턴 문자열 내에서 본 적이 있는 거 같습니다.
그래서 테이블을 확인해 보니 0번에 존재한다는군요.
그럼 다음과 같은 연산을 진행하여 현재의 다음 비교할 위치를 구합니다.
다음 위치 = 본문 문자열 내 현재 INDEX + (패턴 문자열 내의 현재 위치 - 테이블에서 참조한 값)
대입한 결과 : 3 = 0 + (3 +0)
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| m | a | b | c | a | b | a | b | c | d |
| n | a | b | c | d |
그다음에도 일치하지 않는 내용이 발생했습니다.
다음 테이블은 직접 계산해 보고 그려보시는 편이 이해하시는데 도움이 될 거 같습니다.
저희는 첫 번째 방식인 Bad Character Heuristica을 알아봤습니다.
하지만 이와 같은 방식으로만 동작하기에는 정상적으로 동작하지 않는 경우도 발생합니다.
그리고 한 가지 테이블을 더 사용하여 두 테이블 중 더 큰 값으로 넘어간다면 좀 더 반복 횟수를 줄일 수 있을 것입니다.
2. Good Suffix Heuristica
이 방식은 접미사와 같은 문자열이 패턴 문자열 내에 존재하는지 를 검사합니다.
여기서 잠깐 접미사란 문자열 내에서 시작이 어디든 항상 끝까지 나타낸 문자열을 뜻합니다.
아래는 ababcabc에 대한 접미사를 나열한 모습을 보여줍니다.
| ababcabc | 접미사 |
| c | |
| bc | |
| abc | |
| cabc | |
| bcabc | |
| abcabc | |
| babcabc | |
| ababcabc |
그렇다면 접미사와 일치한다는 문자열이란 아래와 같습니다.
| 접미사 | 일치한 문자열 |
| c | ababcabc |
| bc | ababcabc |
| abc | ababcabc |
접미사와 같은 문자열이 무엇인 지 알았으니 아래 테이블은 위의 내용을 테이블로 만든 내용입니다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| pattern | a | b | a | b | c | a | b | c |
| value | 8 | 8 | 5 | 6 | 7 | 8 | 8 | 8 |
접미사와 같았던 문자열이 접미사를 가리키고 있는 것을 확인할 수 있습니다.
하지만 이것만으로 부족합니다. 그 이유는 보이어-무어 알고리즘은 뒤에서부터 비교를 해 나아가기 때문에 저 뒤의 접미사 부분이 바꿉니다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| pattern | a | b | a | b | c | a | b | c |
| value | 8 | 8 | 8 | 8 | 8 | 3 | 8 | 8 |
나머지 값이 패턴 문자열의 길이인 이유는 보이어-무어는 뒤에서부터 비교하기 때문에 틀리면 패턴의 문자열만큼 과감하게 건너뛸 수 있습니다.
위의 테이블은 접미사의 인덱스를 나타냈지만 지금 테이블은 다음 인덱스를 얼마큼 더해서 시작할지를 알려줍니다.
위와 같은 내용으로 c++ 언어로 구현해 보면서 부족한 설명을 해보겠습니다.
구현
1. Bad Character에 대한 테이블을 정의합니다.
Bad Table 은 위에서 설명한 바로 각 문자에 대해 순서대로 번호를 붙여준다고 했습니다.
const int MAX_SIZE = 256;
vector<int> make_to_bad_character_tb(const string pattern){
const int p_size = pattern.size();
vector<int> bc_tb(MAX_SIZE, p_size);
for(int i = 0; i < p_size; ++i)
bc_tb[(int)pattern[i]] = i;
return bc_tb;
}
이 테이블의 문제점은 중복된 문자가 나올 시 기존의 값을 덮어쓴 다했습니다.
반복문 내용을 보시면 받은 문자를 int형으로 바꾼 위치에 값을 저장하는 모습을 볼 수 있을 것입니다.
2. Good Suffix에 대한 테이블을 만듭니다.
vector<int> make_to_gs_tb(const string pattern){
const int p_size = pattern.size();
int pattern_point = p_size;
int suffix_point = pattern_point + 1;
// 접미사와 동일한 문자열 체크하는 테이블
vector<int> suf_tb(p_size + 1, 0);
suf_tb[pattern_point] = suffix_point;
// 생략할 테이블
vector<int> skip_tb(p_size + 1, 0);
while(pattern_point > 0){
// 접미사가 일치하는 순간 몇개가 일치하는지 카운팅
while(suffix_point <= p_size &&
pattern[pattern_point - 1] != pattern[suffix_point -1]){
if(skip_tb[suffix_point] == 0)
skip_tb[suffix_point] = suffix_point - pattern_point;
suffix_point = suf_tb[suffix_point];
}
// 접미사와 동일한 단어가 접미사인덱스를 가르키도록 설정
suf_tb[--pattern_point] = --suffix_point;
}
...
}
위의 코드는 접미사와 동일해질 때 카운트를 시작하여 그에 맞게 배열에 넣어주는 코드입니다.
코드가 한눈에 안 들어와 저도 많이 보고 또 보았습니다.
접미사와 동일한 문자들이 접미사의 인덱스를 가르치도록 만드는 작업이 이루어지는 작업과 일치한 접미사를 찾았을 때 그 얼마큼 스킵할지 저장합니다.
그러면 아래와 같은 테이블이 만들어집니다.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| pattern | a | b | a | b | c | a | b | c | |
| suf_tb | 8 | 8 | 5 | 6 | 7 | 8 | 8 | 8 | 9 |
| skip_tb | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 |
위에서 본 테이블과 많이 비슷해졌습니다.
하지만 아직 생략 테이블은 나머지 문자에 대해서 어떻게 스킵해야 할지 모릅니다.
그렇다면 여기서 한 가지 더 설명드리겠습니다.
suf_tb의 목록을 보시면 일치한 값들이 보입니다. 이 값들은 패턴 문자열의 사이즈와 같으면 그 자릿수만큼 생략이 가능하다는 것입니다. 그리고 이 값은 앞자리부터 채워줍니다.
vector<int> make_to_gs_tb(const string pattern){
const int p_size;
int pattern_point = p_size;
int suffix_point = pattern_point + 1;
// 접미사와 동일한 문자열 체크하는 테이블
vector<int> suf_tb(p_size + 1, 0);
// 생략할 테이블
vector<int> skip_tb(p_size + 1, 0);
...
suffix_point = suf_tb[0];
while(pattern_point < p_size){
if(skip_tb[pattern_point] == 0)
skip_tb[pattern_point] = suffix_point;
if(pattern_point++ == suffix_point)
suffix_point = suf_tb[suffix_point];
}
return skip_tb;
}
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| pattern | a | b | a | b | c | a | b | c | |
| suf_tb | 8 | 8 | 5 | 6 | 7 | 8 | 8 | 8 | 9 |
| skip_tb | 8 | 8 | 8 | 8 | 8 | 3 | 8 | 8 | 0 |
그리고 이렇게 나온 값으로 원하는 문자열 검색을 합니다.
그렇다면 테이블 두 개를 어떠한 방식으로 참조하느냐도 중요합니다.
테이블을 참조하여 가장 큰 값을 택한다 생각하시면 됩니다.
int search(const vector<int> bc_tb, const vector <int> gs_tb,
const string H, const string pattern){
const int h_size = H.size();
const int p_size = pattern.size();
int begin = 0;
if(h_size < p_size) return -1;
while(begin <= h_size - p_size){
int matched = p_size;
while(matched > 0 && pattern[matched - 1] == H[begin + (matched - 1)]){
--matched;
}
if(matched == 0) return begin;
if(bc_table[H[begin + matched]] != p_size){
begin += max(matched - bc_tb[H[begin + matched]],
gs_tb[matched]);
}else{
begin += max(gs_tb[matched], matched);
}
}
return -1;
}
전체 코드
#include <iostream>
#include <vector>
using namespace std;
const int MAX_SIZE = 256;
vector<int> make_to_bad_character_tb(const string pattern)
{
const int p_size = pattern.size();
vector<int> bc_tb(MAX_SIZE, p_size);
for (int i = 0; i < p_size; ++i)
bc_tb[(int)pattern[i]] = i;
return bc_tb;
}
vector<int> make_to_gs_tb(const string pattern)
{
const int p_size = pattern.size();
int pattern_point = p_size;
int suffix_point = pattern_point + 1;
// 접미사와 동일한 문자열 체크하는 테이블
vector<int> suf_tb(p_size + 1, 0);
suf_tb[pattern_point] = suffix_point;
// 생략할 테이블
vector<int> skip_tb(p_size + 1, 0);
while (pattern_point > 0)
{
cout <<'h'<<endl;
// 접미사가 일치하는 순간 몇개가 일치하는지 카운팅
while (suffix_point <= p_size &&
pattern[pattern_point - 1] != pattern[suffix_point - 1])
{
if (skip_tb[suffix_point] == 0)
skip_tb[suffix_point] = suffix_point - pattern_point;
suffix_point = suf_tb[suffix_point];
}
// 접미사와 동일한 단어가 접미사인덱스를 가르키도록 설정
suf_tb[--pattern_point] = --suffix_point;
}
suffix_point = suf_tb[0];
while (pattern_point < p_size)
{
if (skip_tb[pattern_point] == 0)
skip_tb[pattern_point] = suffix_point;
if (pattern_point++ == suffix_point)
suffix_point = suf_tb[suffix_point];
}
for(auto & suf : suf_tb)
cout << suf << ", ";
cout << endl;
for(auto & skip : skip_tb)
cout << skip << ", ";
cout << endl;
return skip_tb;
}
int search(const vector<int> bc_tb, const vector<int> gs_tb,
const string H, const string pattern)
{
const int h_size = H.size();
const int p_size = pattern.size();
int begin = 0;
if (h_size < p_size)
return -1;
while (begin <= h_size - p_size)
{
int matched = p_size;
while (matched > 0 && pattern[matched - 1] == H[begin + (matched - 1)])
{
--matched;
}
if (matched == 0)
return begin;
if (bc_tb[H[begin + matched]] != p_size)
{
begin += max(matched - bc_tb[H[begin + matched]],
gs_tb[matched]);
}
else
{
begin += max(gs_tb[matched], matched);
}
}
return -1;
}
int main()
{
const string h = "abaabaababbabababcabccaabcabcabcbcabcbacba";
const string pattern = "abbab";
const int p_size = pattern.size();
const vector<int> bc_table = make_to_bad_character_tb(pattern);
const vector<int> gs_table = make_to_gs_tb(pattern);
cout << search(bc_table, gs_table, h, pattern) << endl;
return 0;
}
끝맺음
보이어-무어 알고리즘은 타 알고리즘에 비해 저도 이해하는데 상당히 오래 걸렸습니다.
지금도 긴가 민가 하는 부분도 종종 생깁니다.
이렇게 한번 정리를 했어도 저 또한 제 글을 또다시 찾아 읽어보고 좀 더 쉽게 설명할 방안이 없나 생각을 더 해봐야 할거 같습니다.
틀린 부분이 있다면 과감히 지적해주시면 감사하겠습니다.
긴 글 읽어주셔서 감사합니다.

'알고리즘' 카테고리의 다른 글
| [프로그래머스] 단어 변환 - DFS(깊이 탐색) 방식(feat.cpp) (0) | 2020.11.09 |
|---|---|
| [KMP] 카누스 모리스 프렛 알고리즘 (feat.cpp) (0) | 2020.11.04 |
| 트라이 알고리즘이란 ? (feat.cpp) (0) | 2020.11.03 |
| [프로그래머스] 위장 (0) | 2020.11.02 |
| [heap] 힙 이란? (feat.cpp) (0) | 2020.11.01 |
FTP란 무엇인가 ?

FTP 란?
FTP란 File Transfer Protocol의 약자로 영어 그대로 서버와 클라이언트 사이에서 TCP/IP를 통해 파일을 송수신하기 위해 고안된 프로토콜입니다.
해당 프로토콜은 오로지 빠른 파일 송수신만을 목적으로 두고 고안되었기 때문에 보안 부분에서는 상당히 취약한 프로토콜입니다. (보안 취약점에 대해서는 여기를 클릭 시면 됩니다.)
나는 한 개가 아니라 두 개야!
FTP는 다른 프로토콜들과 다르게 포트(port) 번호를 기본 두 개를 사용하도록 제작되었습니다.
첫 번째 포트는 포트번호 21번으로 클라이언트와 서버 사이의 명령, 제어 등을 송수신하는 제어 포트입니다.
그리고 두 번째 포트로는 20번으로 클라이언트와 서버 사이의 직접적인 파일 송 수신을 담당하는 데이터 포트입니다.

PI : Protocol Interpreter의 약자 / DTP : Data Transfer Process의 약자
위 그림은 FTP Model입니다.
1. User PI가 Control connection을 통해 명령(command)을 보냅니다.
2. command를 받은 Server PI는 그에 대하여 응답(Reply)을 보내줍니다.
3. 명령을 받은 Server는 Data connection(전 이중 통신입니다.)을 생성하여 User와 연결하며 데이터 송 수신을 진행하고 진행이 완료된 Data connection은 다시 제거합니다.
이러한 동작으로 인하여 21번 포트인 제어 포트는 첫 연결부터 서로 연결이 끊길 때까지 이어져 있고 20번 포트인 데이터 포트는 명령을 받고 그 명령을 수행하기 위해 포트를 연결한 후 수행이 끝나면 연결된 포트를 제거합니다.
나는 모드도 두 개야!
FTP는 기본 설정으로는 Active mode로 설정되어 있습니다.
FTP는 위에서 포트가 두 개를 사용한다는 것을 저희가 알았습니다.
하지만 이러한 타 프로토콜과 다른 이유 때문에 모드도 두 개가 존재합니다.
처음 연결을 시도할 때 21번 포트로 서로 신호를 주어 받고 그 후 데이터 포트를 연결할 때 Active mode는 클라이언트가 서버에게 20번 포트로 연결해달라고 알려주면 서버는 클라이언트의 20번 포트로 연결을 하는 것입니다.
하지만 이러한 동작은 실제로 방화벽으로 인하여 연결이 제대로 이어지지 않는 일이 발생할 때가 있습니다.
그 때문에 존재하는 것이 Passive mode입니다.
Passive mode는 Active mode의 반대로 서버 쪽에서 클라이언트에게 연결할 포트를 알려줍니다
지금까지의 내용을 요약해 보겠습니다.
FTP는 사용하는 포트가 2개 존재합니다.
1. 제어 포트
2. 데이터 포트.
FTP 사용하는 모드가 2개 존재합니다.
1. Active mode : 클라이언트가 서버에게 연결할 데이터 포트를 알려주는 모드
2. Passive mode : 서버가 클라이언트에게 연결할 데이터 포트를 알려주는 모드
나는 솔직해서 문제야...
위에서 언급했듯이 FTP 프로토콜은 보안이 매우 취약합니다.
서버와 클라이언트가 서로 명령이나 데이터를 주고받을 때 암호화 과정 없이 평문을 주고받습니다.

위 그림은 FTP로 서버에 접속하려는 유저 아이디와 패스워드를 서버에 보내어 인증을 받는 장면입니다.
얼핏 보면 인증도 잘 받고 괜찮아 보입니다.

하지만 위 그림처럼 H라는 해커가 중간에서 가로챈다면 암호화가 하나도 되지 않은 계정 아이디와 패스워드를 확인할 수 있습니다.
FTP 전용 계정이라 괜찮다? 절대 아닙니다.
FTP 주목적이 파일 관리이기 때문에 파일을 삭제하거나 중요 데이터를 삭제, 다운로드 등 큰 문제로 이어질 수 있습니다.
다행히도 현재는 이러한 문제를 해결하기 위해 보안 프로토콜 등이 많이 존재합니다.
아래는 RFC2577에 기재되어있는 보안 취약점에 대한 내용입니다.
무차별 대입 공격(Brute Force)
비밀번호 4개 달린 자물쇠를 다들 아십니까? 예전에 저는 이것을 풀기 위해 0000부터 9999 번호까지 쭉 돌려보기도 해 보았습니다. 이 방법이 무차별 대입 공격입니다.
id와 password를 무작위로 대입해서 공격하는 기법입니다.
FTP Bounce Attack
FTP 프로토콜은 목적지를 별로 중요시 생각하지 않습니다.
무슨 뜻이냐 하면 만약 제가 쇼핑몰에서 물건을 구매했을 때 그 물건은 목적지인 저에게 배송되어야 합니다.
이 과정에서 물건을 보내는 사람은 물건을 시킨 사람의 주소와 목적지의 주소가 같은 지 확인 후 택배를 보낼 것입니다.
그 과정은 FTP 프로토콜은 하지 않습니다. 그러한 점을 이용한 공격이라 보시면 되겠습니다.
위에 공격들 말고도 스니핑, 스푸핑 등 공격들이 있습니다.
명령, 제어 신호
FTP 클라이언트에서 명령을 내리면 그에 따라 응답신호를 보내줍니다.

FTP 명령
USER, PASS
처음 클라이언트와 서버가 연결될 때 이 두 개를 통해 username, password를 보내어 인증을 받습니다.
CWD : 작업 디렉터리를 변경합니다.
CDUP : 부모 디렉터리로 위치를 변경합니다.
RMD : 디렉터리 제거
MKD : 디렉터리 생성
명령어는 더 있지만 주로 사용되는 명령어들을 적어 봤습니다.
끝맺음
이번에 toy project로 ftp client를 제작해 볼 겸 조사한 내용들을 적어봤습니다.
잘못된 정보나 부족한 부분을 지적해 주시면 감사하겠습니다.
[KMP] 카누스 모리스 프렛 알고리즘 (feat.cpp)

K.M.P 알고리즘 이란?
m이라는 문자열 안에 n라는 문자열이 포함되는지 알고 싶은 경우 제일 먼저 생각나는 방법으로는
완전 탐색(Brute Force) 알고리즘이 먼저 생각날 것입니다.
완전 탐색은 간단한 구현만으로도 정확하게 문자열을 찾아낼 수 있지만 길이가 길어질수록 시간이 오래 걸립니다.
m 문자열 길이에 n 문자열 길이만큼 비교하게 되니 시간 복잡도는 O(mn)이나 나옵니다.

KMP 알고리즘은 저런 비교 결과들을 활용 하여 빠르게 문자열의 어느 INDEX 부터 시작할지를 결정합니다.
아래 표를 보시면 첫 매칭에서 A B C A 까지는 맞지만 나머지가 틀려서 찾지못한 결과입니다.
| INDEX | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| M | A | B | C | A | A | B | C | A | B |
| N | A | B | C | A | B |
만약 완전 탐색으로 탐색을 진행했다면, 아래쳐럼 INDEX 1로 이동하여 비교를 진행할것입니다.
| INDEX | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| M | A | B | C | A | A | B | C | A | B |
| N | A | B | C | A | B |
하지만 KMP은 위에 A B C A 까지 맞은것을 이용하여 A (접두사, 접미사 일치) 한 곳부터 시작을 합니다.
| INDEX | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| M | A | B | C | A | A | B | C | A | B |
| N | A | B | C | A | B |
접두사, 접미사
정보를 활용할 수 있는 방법으로는 접두사 (PREFIX)와 접미사 (SUBFIX)가 같은 지점을 찾습니다.
| ABCAB | 접두사 | 접미사 |
| A | B | |
| AB | AB | |
| ABC | CAB | |
| ABCA | BCAB | |
| ABCAB | ABCAB |
맨 아래 ABCAB는 정보를 찾은 결과이니 제외하고 접두사와 접미사가 같은 부분을 찾아보면 AB 가 있습니다.
이 정보를 가지고 생각해봅시다.
만약에 비교중에 접미사 부분에 포함된 부분이 일치하지만 나머지가 틀렸다면 시작 위치를 접미사로 옮겨도 되지 않을까요?
접미사와 접두사가 같다는 뜻은 시작 위치 값 = 끝나는 위치 값 같다 라는 말입니다.
구현
1. n(찾을 문자열)에 대하여 접두사와 접미사가 같은 부분을 찾습니다.(PI 테이블 생성)
begin : 접미사 시작 부분
matched : 접두사 시작 부분
vector<int> get_pi(const string n){
const int n_size = n.size();
int begin = 1, matched = 0;
vector<int> pi(n_size, 0);
while(begin + matched < n_size){
if(n[begin + matched] == n[matched]){
++matched;
pi[begin + matched - 1] = matched;
}else{
if(matched == 0){
++begin;
}else{
begin += matched - pi[matched - 1];
matched = pi[matched - 1];
}
}
}
return pi;
}

2. 문자열을 비교하고 만약 매칭이 되지 않을 시 PI테이블을 보고 시작할 위치를 정합니다.
ret : 찾는 패턴의 시작 위치들을 담고 있는 변수
vector<int> search_to_pettern(const string m, const string n){
vector<int> ret;
const int m_size = m.size();
const int n_size = n.size();
const vector<int> pi = get_pi(n);
int begin = 0, matched = 0;
while(begin + matched < m_size){
if(matched < n_size && m[begin + matched] == n[matched]){
++matched;
if(matched == n_size)
ret.push_back(begin);
}else{
if(matched == 0)
++begin;
else{
begin += matched - pi[matched - 1];
matched = pi[matched - 1];
}
}
}
return ret;
}
전체 코드
#include <iostream>
#include <vector>
using namespace std;
vector<int> get_pi(const string n){
const int n_size = n.size();
int begin = 1, matched = 0;
vector<int> pi(n_size, 0);
while(begin + matched < n_size){
if(n[begin + matched] == n[matched]){
++matched;
pi[begin + matched - 1] = matched;
}else{
if(matched == 0){
++begin;
}else{
begin += matched - pi[matched - 1];
matched = pi[matched - 1];
}
}
}
return pi;
}
vector<int> search_to_pettern(const string m, const string n){
vector<int> ret;
const int m_size = m.size();
const int n_size = n.size();
const vector<int> pi = get_pi(n);
int begin = 0, matched = 0;
while(begin + matched < m_size){
if(matched < n_size && m[begin + matched] == n[matched]){
++matched;
if(matched == n_size)
ret.push_back(begin);
}else{
if(matched == 0)
++begin;
else{
begin += matched - pi[matched - 1];
matched = pi[matched - 1];
}
}
}
return ret;
}
테스트 코드 (필요하신 분만(
int main(){
const string m = "aabaabacabaaaabaabac";
const string n = "aabaabac";
const vector<int> ret = search_to_pettern(m, n);
for(auto & num : ret){
cout << num << endl;
}
return 0;
}

'알고리즘' 카테고리의 다른 글
| [프로그래머스] 단어 변환 - DFS(깊이 탐색) 방식(feat.cpp) (0) | 2020.11.09 |
|---|---|
| [Boyer-Moore] 문자열 탐색 ! 보이어-무어 알고리즘(feat.cpp) (0) | 2020.11.07 |
| 트라이 알고리즘이란 ? (feat.cpp) (0) | 2020.11.03 |
| [프로그래머스] 위장 (0) | 2020.11.02 |
| [heap] 힙 이란? (feat.cpp) (0) | 2020.11.01 |
트라이 알고리즘이란 ? (feat.cpp)

트라이 란?
문자열 탐색을 보다 효율적으로 하기 위해 고안된 알고리즘입니다
단순하게 문자열을 비교해 나가면(brute force) 문자열 길이가 길어질수록 수행 시간이 오래 걸립니다..
반면 트라이 알고리즘은 트리 형태로 문자열을 정리해놓아 탐색 시 빠르게 탐색할 수 있습니다.
단. 트라이 알고리즘은 문자열의 길이가 길어질수록 트리의 깊이도 깊어지므로 공간 복잡도가 안 좋습니다.
아래 사진은 tree라는 문자열을 Insert 하는 과정입니다.

구현 - alpabet 소문자 기준
1. 트라이 클래스 생성
node : 자식 노드를 가리키는 변수(다음 문자를 가리킨다.)
check_end_str : 문자열의 마지막인지 아닌지 체크하는 변수
#define MAX_TRIE_SIZE 26
class Trie{
public :
Trie * node[MAX_TRIE_SIZE];
bool check_end_str;
Trie(){
fill(node, node + MAX_TRIE_SIZE, nullptr);
check_end_str = false;
}
~Trie(){
for(int i = 0; i < MAX_TRIE_SIZE; ++i)
if(node[i] != nullptr)
delete node[i];
}
...
};2. INSERT()
위에서 노드를 보면 26개의 배열로 만들어졌습니다.(알파벳 개수는 26개)
즉, a문자는 node [0], b문자는 node [1]... z문자는 node [25]에 값을 할당해 주기 위함입니다.
그러기 위해서는 알파벳을 노드의 인덱스로 바꾸어 주어야 합니다.
class Trie{
...
int translate_index(const char c){
return c - 'a';
}
...
};
입력받은 문자가 마지막('\0') 일 시 check_end_str을 true 바꾸어 마지막임을 표시합니다.
마지막 문자에 도달할 때까지 노드를 만들거나 기존 노드를 타고 이동합니다.
class Trie{
...
void insert(const char * str){
if(*str == '\0'){
check_end_str = true;
}else{
const int index = translate_index(*str);
if(node[index] == nullptr)
node[index] = new Trie();
node[index]->insert(str + 1);
}
}
...
}
2. find()
트라이 탐색은 INSERT와 다른 점은 반환하는 값이 있다는 것뿐입니다.
마지막 문자열까지 도달했을 경우 문자열을 찾은 것이니 true을 리턴,
만약 마지막 문자열이 아니지만 해당 노드가 비어있다면 false를 리턴하도록 하겠습니다.
class Trie{
...
bool find(const char * str){
if(*str == '\0')
return true;
const int index = translate_index(*str);
if(node[index] == nullptr)
return false;
node[index]->find(str + 1);
}
...
}
전체 코드
#include <iostream>
#include <algorithm>
#define MAX_TRIE_SIZE 26
using namespace std;
class Trie{
public :
Trie * node[MAX_TRIE_SIZE];
bool check_end_str;
Trie(){
fill(node, node + MAX_TRIE_SIZE, nullptr);
check_end_str = false;
}
~Trie(){
for(int i = 0; i < MAX_TRIE_SIZE; ++i)
if(node[i] != nullptr)
delete node[i];
}
int translate_index(const char c){
return c - 'a';
}
void insert(const char * str){
if(*str == '\0'){
check_end_str = true;
}else{
const int index = translate_index(*str);
if(node[index] == nullptr)
node[index] = new Trie();
node[index]->insert(str + 1);
}
}
bool find(const char * str){
if(*str == '\0')
return true;
const int index = translate_index(*str);
if(node[index] == nullptr)
return false;
node[index]->find(str + 1);
}
};
테스트 코드 (필요하신 분만)
words : trie에 저장할 문자열 목록
find_words : 탐색할 문자열 목록
int main(){
Trie * trie = new Trie();
const vector<string> words = {
"apple", "tree", "word", "fire", "egg", "people", "number",
"py", "google", "naver", "daum", "tistory"
};
const vector<string> find_words = {
"apple", "tr", "google", "go", "whole", "find", "num",
"good", "job", "peo", "never", "naver", "py", "pi"
};
// insert
for(auto & word : words){
trie->insert(word.c_str());
}
for(auto & find_word : find_words){
cout << find_word;
if(trie->find(find_word.c_str()))
cout << " is!!!";
else
cout << " isn't...";
cout << endl;
}
return 0;
}

'알고리즘' 카테고리의 다른 글
| [Boyer-Moore] 문자열 탐색 ! 보이어-무어 알고리즘(feat.cpp) (0) | 2020.11.07 |
|---|---|
| [KMP] 카누스 모리스 프렛 알고리즘 (feat.cpp) (0) | 2020.11.04 |
| [프로그래머스] 위장 (0) | 2020.11.02 |
| [heap] 힙 이란? (feat.cpp) (0) | 2020.11.01 |
| [프로그래머스] 가장 큰 수 (0) | 2020.10.30 |

